Франсуа Шмитц - Витгенштейн [litres]

Столбец под знаком «˅» мы использовали в качестве исходной точки.

Из всего вышеизложенного можно сделать несколько выводов, которые приводит Витгенштейн.

– Не существует логической константы.

Прежде всего, представляется очевидным, что пропозициональные связки взаимовыразимы. Например, предложение если р, то q(p → q) имеет ту же «истинностную функцию» р и q, что и предложение не р или q (~p ˅ q), и не (р и не q) (~( p ˄ ~q)). Так что достаточно воспользоваться связками «~» и «˅» или «~» и «→», а то и вовсе одной связкой «↓», чтобы записать какое угодно молекулярное предложение, состоящее из двух элементарных предложений. Из этого следует, что нет никаких оснований для того, чтобы присваивать этим связкам особое значение; единственное, что важно, – знать, какая «истинностная функция» элементарных предложений есть молекулярное предложение, что в случае с p → q становится очевидным посредством обозначения (и, л, и, и,) (p, q), без каких-либо связок. Напротив, использование логических союзов может запросто навести на мысль, что они обладают особым значением, обозначая то, что Рассел называл «логическими данными».

Теперь мы лучше понимаем «основополагающую идею» Витгенштейна: не существует ни логического «объекта», ни логической константы, а логика как наука не должна заниматься изучением свойств этих так называемых объектов. По сути использование логических союзов создает иллюзию, что они сообщают нечто о форме (то есть условиях истинности) молекулярных предложений, которые образуются с их помощью, и это приводит к колоссальной путанице, в которую оказались втянуты Фреге с Расселом (и не только они одни!).

Второй вывод, который можно сделать при изучении нашей таблицы, касается способа ее построения. Мы использовали несложный пример истинностных функций двух элементарных предложений. Однако мы можем проделать абсолютно то же самое с бесчисленным множеством элементарных предложений: имея n элементарных предложений, можно последовательно создать все истинностные функции этих n предложений. В отношении этих n элементарных предложений существуют 2 nвозможности истинности, соответствующие тем же 2 nвозможностям существования или несуществования положений вещей, отображаемых n элементарных предложений. Простой подсчет показывает, что имеется 2 (2n)различных истинностных функций n элементарных предложений.

Однако пойдем дальше: как мы видели, можно выразить все истинностные функции при помощи истинностных функций лишь двух элементарных предложений. Между тем все истинностные функции двух элементарных предложений могут, в свою очередь, быть выражены посредством, например, одной функции – «инверсии» («ни… ни…», которую иногда называют штрихом Шеффера по имени ее «изобретателя»). Из этой возможности Витгенштейн выводит то, что составляет стержень «Трактата»: совокупность молекулярных предложений можно определить как результат одной операции – инверсии – над элементарными предложениями.

Вместо этой чересчур простой операции попробуем пояснить мысль Витгенштейна посредством двух операций – отрицания и дизъюнкции. Для большей наглядности предположим, что существует только три элементарных предложения – p, q и r. Из этих трех предложений мы условимся образовывать новые предложения, либо ставя знак отрицания «~» перед одним предложением, либо вставляя знак дизъюнкции «v» между двумя предложениями. Итак, вот пример того, как можно строить более сложные предложения:

– p; ~ p ˅ q; ~ (~ p ˅ q); r ˅ ~ (~ p ˅ q); ~q; ~q ˅ [ r ˅~ (~ p ˅ q) ] и т. д.

Таким образом возможно сконструировать a priori все истинностные функции одного, двух или трех элементарных предложений. Главное заключается в том, что способ, которым мы строили пропозициональные знаки, позволяет обнаружить на каждом этапе данного построения условия истинности нового предложения, поскольку каждое из двух обозначений операций одновременно является выражением определенной истинностной функции (см. таблицу, приведенную выше). В отношении выбранных нами примеров результат будет следующим: ~ p является истинным, если, и только если p является ложным; ~ p ˅ q является истинным, если, и только если ~ p и q не являются одновременно ложными, иначе говоря, если p не является истинным, а q ложным; ~ ( ~ p ˅ q) является истинным, если, и только если ~ p ˅ q является ложным, другими словами, если… и т. д.

Разумеется, мы ограничились тремя элементарными предложениями только из педагогических соображений, и этот способ может иметь широкое применение. Из всего вышеизложенного Витгенштейн вывел то, что он называет «общей формой предложения», которая представляет все пропозициональные (молекулярные) формы посредством логической символики: 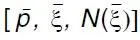, в котором 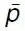обозначает совокупность элементарных предложений, 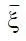– совокупность предложений (элементарных или полученных из элементарных посредством операции N ), а N ( 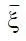) – результат выполнения операции инверсии по отношению к .

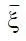Таким образом, данная общая форма предложения, беря в расчет лишь форму предложений, предъявляет in nucleo все возможные пропозициональные формы; она является выражением правила знаков и в то же время показывает условия истинности каждого нового предложения. Другими словами, она позволяет a priori сконструировать форму из других форм с помощью единственной операции инверсии. В этом смысле, ничего не говоря об этих формах, она ограничивается тем, что показывает их.

Именно большой успех «Трактата» придал смысл главной идее, к которой нас подвело рассмотрение понятия образа, а именно – к тому, что логическая форма является невыразимой и может лишь показывать себя в соответствующей символике. Отсюда возникает вопрос: если можно показать пропозициональный знак через него самого, каковы условия истинности предложения?

На этом не заканчиваются выводы, вынесенные Витгенштейном из своего тезиса, согласно которому не следует признавать какие-либо логические константы. Теперь пришел черед обратиться к двум столбцам таблицы истинности. Эти столбцы демонстрируют странность, которая заключается в согласовании, выраженном соответствующими предложениями со всеми истинностными возможностями элементарных предложений (или ни с одной из них). Это означает, что данные предложения в действительности не имеют условий истинности, поскольку они либо всегда истинны (тавтология), либо всегда ложны (противоречие), независимо от того, что имеет место в действительности. Обычное предложение, наоборот, является истинным лишь при определенных условиях, с которыми оно согласуется, или ложным, если одно из этих условий не было выполнено. Между тем мы многократно настаивали на том, что смыслом предложения являются его условия истинности. Из этого непосредственно вытекает, что предложение, не имеющее условий истинности, – бессмысленно. Может показаться, что составленная нами таблица так же позволяет строить предложения, лишенные смысла, как и естественный язык…