Борис Шулицкий - Мадэализм — концепция мировоззрения III тысячелетия (заметки по поводу модернизации физической теории)

Но теория развития не остановилась на представлениях эпохи Возрождения. Глубокую философскую разработку она получила в немецкой классической философии XVIII—XIX в.в., особенно у Гегеля, «открывшего», по словам К. Маркса, и построившего диалектику как учение о всеобщем развитии духа. «Диалектический метод, — утверждает Гегель, — есть душа всякого научного развертывания мысли», именно он и только он «вносит необходимую внутреннюю связь в содержание науки» (53,63). Дальнейшую разработку, уже в материалистическом аспекте, учение о развитии получило в марксизме, трактующем развитие как универсальное свойство материи и, вместе с тем, как всеобщий принцип, служащий основой объяснения истории общества и познания. Показана всеобщность, универсальность диалектического механизма процессов развития. Однако до настоящего времени эти философские разработки не нашли адекватного отражения в математическом аппарате , то есть не «переведены» на язык науки и, соответственно, не доступны современному естествознанию .

Между тем одна из актуальнейших дискуссионных проблем современного естествознания — проблема «нарушения причинности», потери детерминизма на микроуровне, проблема соотношения причины и следствия (74). В собственно математике это так называемый «третий кризис основ», связанный с теорией множеств и соотношением части и целого (9). Проблемы части и целого возникли и в квантовой физике. Не имеют ли эти проблемы общих корней?

В каком же направлении искать пути выхода из кризиса? Может быть, исторически проверенным методом — использовать философию как матрицу научного поиска?

Используя историческую аналогию, можно предположить, что в математике должен появится новый теоретический уровень , который отразит универсальный всеобщий диалектический характер процессов движения, изменения, развития, совершающегося в соответствии со всеми требованиями развертывания диалектического противоречия. Тем самым математика переведет на язык науки тот потенциал диалектической теории, который накоплен человечеством за последние несколько столетий. В этом, конечно, есть серьезные трудности, так как «противоречие, — по словам Гегеля, — выступает непосредственно лишь в определении отношения. А в движении, импульсе и т.п. противоречие скрыто для представления за простотой этих определений». Но, тем не менее, «все вещи противоречивы в самих себе». «Противоречие — это имманентный источник движения, развития. Это принцип всякого самодвижения». «Противоречие — вот что на самом деле движет миром» (23).

Согласно мадэалистической концепции, в фундаменте любых процессов актуальной действительности лежит универсальный структурный «кирпичик мироздания» — структурный слой. Диалектика структурного слоя, рассмотренная в разделах 7.1 и 7.2, являясь отражением универсального механизма эволюции, заключает в себе мощный методологический потенциал. Появилась возможность создать эквивалентную конструкцию и в математической теории. Предположительно область математики, оперирующую формальными конструкциями такого рода, можно определить как «детерминальное» исчисление . Детерминальное исчисление позволит рассматривать статику и динамику причинно-следственных связей и сделать анализ соотношения части и целого. Детерминальное исчисление уже давно востребовано естествознанием, так как проблемы его (естествознания) модернизации связаны в свою очередь с проблемой модернизации математической теории как языка науки. Детерминальное исчисление предполагает введение новой математической символики, отражающей универсальный диалектический характер любых процессов. Следует заметить, что в истории математики нередко лишь благодаря новому способу записи становились возможными новые результаты, что отражает глубокую зависимость между содержанием и формой. Одним из примеров этого является введение индийско-арабских цифр, другим примером может быть символика Лейбница в анализе. «Лейбниц — один из самых плодовитых изобретателей символов. Немногие так хорошо понимали единство формы и содержания. На этом философском фоне можно понять, как он изобрел анализ: это было результатом его поисков „универсального языка“, в частности языка, выражающего изменение и движение» (5,151). Подходящие обозначения лучше отражают действительность, чем неудачные, и они оказываются как бы наделенными собственной жизненной силой, которая, в свою очередь, порождает новое знание. Таким образом, возможно, требуется введение в математическую теорию новой символики , которая (в рамках детерминального исчисления) отразит универсальный диалектический характер процессов изменения, развития.

Интересно заметить, что в последовательности возникновения основных разделов математики проявляется закон отрицания отрицания (9,70) (см. схему).

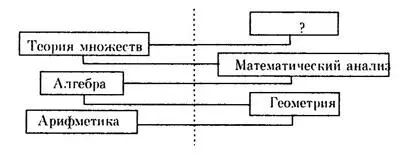
«Так, — пишет Н.И. Жуков, — создание системы символов для обозначения переменных величин в алгебре (работы Ф. Виета), введение буквенного коэффициента в уравнения представляет собой как бы возврат к арифметике, но на новой основе. В свою очередь, возникновение математического анализа есть не что иное, как распространение понятия переменной величины из области дискретного на область непрерывного с последующим освобождением функций от их геометрической интерпретации. Наконец, появление теоретико-множественного подхода определило перенесение центра тяжести снова на область дискретного» (9,70). Таким образом, следующий раздел математики должен перенести центр тяжести опять в область непрерывного, то есть исходить из теории множеств и иметь какие-то аналогии с разделом исчисления бесконечно малых. На наш взгляд, таким разделом может стать детерминальное исчисление.

Математической дисциплиной, наиболее близко подошедшей к осознанию необходимости символьного отражения диалектического характера процессов изменения, развития, является математическая логика. «Идея логического исчисления высказываний, суждений содержалась еще в трудах Лейбница (в работе „Искусство комбинаторики“, например). Однако основы математической логики удалось заложить лишь в XIX веке Дж. Булю, который создал алгебру логики. Впрочем, его работы современниками всерьез не принимались и многими, даже видными, учеными рассматривались как простой курьез, плод досужего ума, в лучшем случае. Одновременно основы новой науки успешно разрабатывал А. Морган, но главным образом — Э. Шредер, так что начиная с конца XIX века она стала называться алгеброй Буля — Шредера. Большой вклад в ее дальнейшее развитие внесли П.С. Порецкий, Фреге, Пеано и, конечно же, известный философ Рассел, который совместно с А. Уайтхедом в начале XX века создал капитальный труд „Принципы математики“. Именно с Фреге и Рассела начинается новый этап в развитии логики как исчисления. С середины XX века она получила особенно большое развитие в связи с успехами кибернетики и информатики и является ныне важнейшей областью математического знания» (9,59).