Жиль Делёз - Складка. Лейбниц и барокко

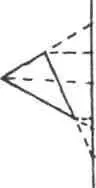
Никто лучше Мишеля Серра не вывел как последствий, так и допущений новой теории конических сечений: в мире бесконечности, или переменной кривизны, потерявшем всякий центр, важно заменить отсутствующий центр на точку зрения: новая оптическая модель перцепции и геометрия в перцепции отвергают

{14}

Об уравнении с двусмысленным знаком, включающим различные случаи конического сечения, ср. «О методе универсальности», С, р. 97 и след.

15Rene Taton, L'reuvre mathematique de Desargues, Vrin, p. 110. Ивонна Торо комментирует это понятие инволюции Дезарга в связи не только с Лейбницем, но и со Спинозой, демонстрируя огромный интерес последнего к теории конических сечений: это проливает совершенно новый свет на спинозизм и «параллелизм». (Yvonne Toros, L'optique de Spinoza, в печати).

{38}

осязательные понятия, контакт и фигуры в пользу «архитектуры видения»; статус объекта таков, что последний существует лишь через собственные метаморфозы или же в разнообразии своих сечений; перспективизм есть истина относительности (а не относительность истины). Дело здесь в том, что точка зрения в каждой области варьирования представляет собой потенцию упорядочивания случаев, условие проявления истинного: таковы чередующаяся серия конических сечений с вершиной конуса как отправной точкой (конечная точка, бесконечная прямая, конечная окружность, бесконечная парабола, конечный эллипс, бесконечная гипербола); или же ряд степеней числа 2, с вершиной арифметического треугольника в качестве отправной точки, — а для всей области варьирования — необходимо указать на основную точку зрения, без которой невозможно обнаружить истину, т. е. сериализовать вариацию или детерминировать случаи. 1Во всех областях Лейбниц строит «таблицы» случаев, отсылающие к точке зрения, как к юриспруденции или к искусству суждения. Нужно всегда находить хорошую, или скорее лучшую, точку зрения, без каковой не было бы ничего, кроме неразберихи и даже хаоса. Когда мы вспомнили Генри Джеймса, то это случилось в связи с лейбницианской идеей точки зрения как тайны вещей, фокуса, тайнописи, — или как детерминации недетерминированного двусмысленными знаками: то, о чем я вам говорю, и о чем вы также думаете — согласны ли вы сказать это о нем, если нам известно, как с этим следует поступить; и о ней, если мы пришли к согласию, кто такой он и кто такая она? Только некая точка зрения — как в барочном анаморфозе

— предоставляет нам и ответы, и случаи.

От переменной искривленности мы перешли к фокусу кривизны (с вогнутой стороны), от вариации — к точке зрения, от складки — к свертыванию, словом, от инфлексии к включению. Этот переход неощутим, что немного напоминает то, как прямой угол измеряется не

16Serres, p. 156–163, II, р. 665–667, 690–695.

{39}

большой, но любой дугой, сколь бы мала и близка к вершине она ни была: «угол или наклонное положение двух линий» содержится уже в вершине. 17И все же мы не решаемся сказать, что видимое находится в точке зрения. Чтобы заставить нас принять эту крайность, необходим более естественный и наглядный пример. Вот простейшая и нагляднейшая интуиция: для чего складывается некая вещь, как не для того, чтобы быть обернутой другой вещью, быть в нее вложенной? Представляется, что именно здесь оболочка обретает свой последний, или, скорее, окончательный, смысл: это уже не оболочка связности или сцепленности, подобная яйцу, где наличествует «взаимообволакивание» органических элементов. Но это, вдобавок, и не математическая оболочка смыкания или присоединения, когда, опять же, одна складка обволакивает остальные, как в случае с огибающей кривой, каковая касается бесконечного множества кривых в бесконечном множестве точек. Это оболочка односторонней присущности или неотъемлемости (inherence, inhesion): конечной целью сгиба является образование включения и присущности, и поэтому от сгиба к присущности мы переходим незаметно. Между ними происходит некий сдвиг, который и превращает оболочку в основную причину сгиба: сгибаемое является включенным и неотъемлемым. Похоже, что сгибаемое лишь виртуально: актуально оно существует лишь в оболочке, внутри некоей обволакивающей его вещи.

Следовательно, неточным было бы сказать, что включает именно точка зрения; или, по крайней мере, она это делает на правах фактора, но не конечной причины и не завершенного действия (энтелехии). Включение и неотъемлемость находятся в состоянии замкнутости или закрытости, о котором Лейбниц высказался в своей знаменитой формуле «нет окон», и для заполнения этого включения точки зрения недостаточно.

{17}

Письмо к курфюрстине Софии, июнь 1700 (GPh, VII, р. 554). Аналогично этому в «Обосновании исчисления…» показано, как в точке А содержится и сохраняется отношение с/е.

{40}

То, в чем происходит и не перестает происходить включение, или то, что включает в смысле завершенного действия, является не позицией, не местом и не точкой зрения, но тем, что пребывает в точке зрения, тем, что точку зрения занимает, тем, без чего точка зрения не стала бы таковой. И этим с необходимостью является душа, субъект. Именно душа всегда включает постигаемое ею со своей точки зрения, т. е. инфлексию. Инфлексия есть идеальность, или виртуальность, которая актуально существует только в «обволакивающей» ее душе. Следовательно, сгибы имеет именно душа, именно она наполнена сгибами. Сгибы находятся в душе, и актуально существуют только в ней. Воистину — это «врожденные идеи»: это чистые виртуальности, чистые потенции, чье действие проявляется в составе или задатках (сгибах) души, и чье завершенное действие состоит в каком-либо действии, совершающемся в душе (внутренний разгиб). 18Это столь же верно и для мира: весь мир — не что иное, как виртуальность, существующая актуально лишь в сгибах выражающей его души, ибо душа действует благодаря внутреннему разгибу, посредством которого она составляет представление о включенном в нее мире. Мы переходим от линии инфлексии к включению в рамках субъекта, как от виртуального к актуальному, так как эта линия определяет сгиб, включение же — душу или субъект, т. е. оболочку сгиба, его конечную цель и завершенное действие.

Отсюда — различие между тремя видами точек, как между тремя типами сингулярностей. 19 Физическая

18В этом смысле Лейбниц различает: виртуальность или идею; модификацию, склонность, предрасположенность или привычку, подобную потенциальному действию в душе; тяготение к поступку и сам поступок как актуализацию действия. Иными словами, пользуясь скульптурной метафорой: фигура Геракла;