Моррис Коэн - Введение в логику и научный метод
- Название:Введение в логику и научный метод
- Автор:
- Жанр:
- Издательство:Социум
- Год:2010
- Город:Москва
- ISBN:978-5-91603-029-7
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Моррис Коэн - Введение в логику и научный метод краткое содержание
На протяжении десятилетий эта книга служила основным учебником по логике и научному методу в большинстве американских вузов и до сих пор пользуется спросом (последнее переиздание на английском языке увидело свет в 2007 г.). Авторам удалось органично совместить силлогистику Аристотеля с формализованным языком математической логики, а методология познания излагается ими в тесной связи с логикой. Освещаются все стандартные темы, преподаваемые в базовом курсе по логике, при этом их изложение является более подробным, чем в стандартных учебниках. Как синтетический курс логики и научной методологии не имеет аналога среди отечественных учебников.
Значительная часть книги посвящена исследованию проблем прикладной логики: экспериментальным исследованиям, индукции, статистическим методам, анализу оценочных суждений.
В книге дается анализ предмета логики и природы научного метода, рассмотрение той роли, которую методы логики играют в научном познании, а также критика многих альтернативных подходов к истолкованию логики и науки в целом. В этом отношении она представляет собой самостоятельное философское произведение и будет интересна специалистам в области философии и методологии науки.
Для преподавателей логики, философии науки, теории аргументации и концепций современного естествознания, студентов, изучающих логику и методологию науки.
Введение в логику и научный метод - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
2. Принцип противоречия :
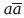
= 0.
Ничто не является членом класса а и одновременно членом класса не-а.
3. Принцип исключенного третьего : а +
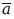 = 1.
= 1.
Каждый индивид универсума либо является членом а, либо членом не-а.
4. Принцип перестановки : аb = Ьа
а + Ь = Ь + а.
Проиллюстрировать данный принцип можно следующим образом: класс индивидов, являющихся одновременно немцами и музыкантами, это то же самое, что и класс индивидов, являющихся одновременно музыкантами и немцами; класс индивидов, являющихся немцами или музыкантами, это то же самое, что и класс индивидов, являющихся музыкантами или немцами.
5. Принцип ассоциации :
( ab ) c = a ( bc ),
( a + b ) + c = a + ( b + c ).
6. Принцип дистрибуции :
( a + b ) c = ac + bc ,
ab + c = ( a + c ) ( b + c ).
В первой строчке выражен аналог хорошо известного свойства обычных чисел. Во второй же вводится значимое различие между предлагаемой алгеброй и ее обычным (вычислительным) видом.
7. Принцип тавтологии :
aa = a ,
a + a = a .
Эти два принципа заключают в себе радикальное различие между обычной (вычислительной) алгеброй и той, что предлагается здесь.
8. Принцип поглощения :
a + ab = a ,
a ( a + b ) = a .
9. Принцип упрощения :
ab < a,
a < a + b .
Из последних двух принципов следует, что нуль-класс включен в любой класс (0 < а) и что любой класс включен в универсум (а < 1). Чтобы наглядно в этом убедиться, нужно всего лишь допустить, что Ь = 0 в первом выражении и что Ь = 1 во втором выражении.
10. Принцип композиции :
[( a < b ) . ( c < d )] ⊃ ( ac ⊃ bd )
[( a < b ) . ( c < d )] ⊃ [( a + c ) < ( b + d )].
Здесь мы, как обычно, используем символ «⊃» для обозначения отношения импликации и точку («.») для обозначения совместного утверждения обоих суждений. Первое выражение читается так: «Если а включен в b и с включен в d , то логическое произведение а и с включено в логическое произведение b и d .
11. Принцип силлогизма :
[( a < b ) . ( b < c )] ⊃ ( a < c ).
Если а включен в Ь и Ь включен в с, то а включен в с. Отношение «включен в» тем самым задается как транзитивное.
Выражение традиционных категорических суждений
Теперь выразим символически каждый из четырех видов категорических суждений.
Суждение «все а суть b» может быть выражено как «(а < b)». Более того, можно показать, что эта запись эквивалентна записи «(аb = 0)». Поэтому мы получаем: «(а <
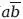
) ≡ (
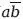
= 0)».
Суждение «ни один а не есть b» эквивалентно суждению «все а суть не‑». Следовательно, символически эта запись может быть выражена как «(a <
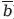
)». Однако данное выражение эквивалентно выражению «(ab = 0)», так что можно получить и следующую запись: «(a <
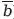
) ≡ (ab = 0)».
Частные суждения противоречат общим, и поэтому в них отрицается то, что утверждается в общих. Поэтому в суждении «некоторые а суть Ь» отрицается то, что ни один а не есть Ь (символически: a <
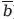
). Это обстоятельство может быть выражено как «(a <
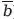
)′» или как «(ab ≠ 0).
Суждение «некоторые а не суть b» должно противоречить суждению (а < b). Следовательно, его можно выразить как «(a < b)′» или как «(
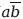
≠ 0)».
Каждая из этих четырех символических форм должна быть знакома читателю по проведенному ранее анализу категорических суждений.
Доказательство теоремы де Моргана В рамках данной книги мы не можем развить исчисление классов, с тем чтобы показать его огромные возможности. Однако мы хотели бы проиллюстрировать природу доказательства в этом исчислении, предложив демонстрацию теоремы де Моргана применительно к классам.
Нам нужно найти дополнение к классу (a + Ь).
В силу принципа исключенного третьего a +
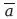
= 1 и Ь +
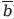
= 1. Также, согласно принципу упрощения, 1x1 = 1 и ∴ (а +
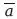
) (Ь +
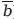
) = 1. Используя принципы дистрибуции и ассоциации, вышесказанное можно записать так: (ab +
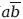
+
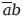
) + (
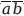
) = 1.
Теперь рассмотрим классы (ab +
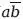
+
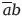
) и (
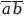
). Они исчерпывают универсум, поскольку их сумма равняется 1; они также являются взаимоисключающими, поскольку их произведение равняется 0. Поэтому любой из них является дополнением другого.
Однако, согласно принципу тавтологии, ab +
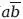
+
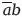
= ab +
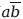
+
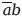
+ ab. Правая часть, по принципу дистрибуции, равна а (Ь +
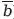
) + Ь (а +
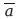
) = а + Ь. Следовательно, поскольку (
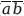
) является дополнением к (ab +
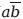
+
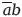
), который, в свою очередь, равен (а + Ь), то, значит, (
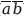
) также равен и (а + Ь).
Следовательно, мы получаем (
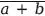
) = (
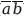
), что является одной из форм теоремы де Моргана.
Теперь попробуем получить дополнение к ab.
Используя аргумент, тождественный только что приведенному, (ab) и (
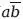
+
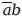
+
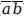
Интервал:
Закладка:










