Сергей Кутолин - Философия интеллекта реального идеализма
- Название:Философия интеллекта реального идеализма
- Автор:
- Жанр:
- Издательство:СГАПС
- Год:1996
- Город:Новосибирск
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Сергей Кутолин - Философия интеллекта реального идеализма краткое содержание
В работе показана роль личности и ее духовных носителей в преодолении трудностей, создаваемых государственными авторитарными системами в эпохи бюрократического засилия.
Философия интеллекта реального идеализма - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
PT № MV + Mў Vў, (3.4)
где P — уровень цен, T — количество товаров и услуг, M — количество денег, V — скорость их обращения, Mў — количество ценных бумаг, Vў — скорость их обращения.
3.2. Рефлексия «финансово-экономического выживания»
Откажемся от линейного вида закона (3.4), хотя, как известно, эта классическая закономерность считается открытой еще в XVIII в. Более того, путем рефлексивного метода [32] найдем новые закономерности между параметрами P , T , MV , Mў Vў для ситуации, когда между финансово-экономическими возможностями h в m случаях (порядок относительного обращения ценностей) и видами технологий q , реализуемых в n вариантах, имеет место равновесие в форме равномощности множеств:
nn = mh . (3.5)
Введем понятие относительного обращения c = MV / Mў Vў как отношения массы денег и скорости их обращения к массе ценных бумаг и скорости их обращения. Тогда уравнение состояния финансово-экономических возможностей будет: h = h ( P , T , c ). Будем характеризовать уровень технологии n = n ( с ), где с — константа скорости конверсии финансово-экономических возможностей системы в заданный уровень технологии или наоборот. По аналогии, например, с известным «законом действия масс» в химии, т.е. заимствуя семиотические возможности «языка химии», будем полагать, что уровень цен P — величина, обратная покупательной силе денег, прямо пропорционален относительному обращению ценностей c в степени порядка m обращения ценностей:
P = cc m = с ( MV / Mў Vў ) m . (3.6)
Предположим, что уровень товаров и услуг T аналогичен закону (3.6) и отличается от него, по крайней мере, не более, чем на порядок относительного обращения ценностей m , т.е.
T = ccmЧ cm = сc 2 m = с ( MV / Mў Vў ) 2 m . (3.7)
Законы (3.6), (3.7), введенные для расчета уровня цен P , товаров и услуг T , представляются достаточно искусственными. Во-первых, они обладают одним и тем же постоянным коэффициентом скорости конверсии финансово-экономических возможностей с, а во-вторых, отличаются по величине порядка относительного обращения m в два раза. Если же воспользоваться достаточно точными экспериментальными данными для P , T , MV , Mў Vў, приведенными, например, в работе [30], то для 16 точек величин P , T , MV , Mў Vў (табл. 3.1) получим данные, свидетельствующие, что законы (3.6), (3.7) действительно реализуются экспериментально, а величины с и m , вычисленные по программам [43], соответственно имеют значения: с = 22,213, m = –0,6307.
Таблица 3.1
Экспериментальные [30] параметры M , Mў, V , Vў, P , T , MV , Mў Vў в уравнении обмена (3.4), используемые для построения закона (3.6) – (3.11) по 16 точкам (годы)
| Годы | M | Mў | V | Vў | P | T | MV | Mў Vў |
|---|---|---|---|---|---|---|---|---|
| 1896 | 0,88 | 2,71 | 18,8 | 36,6 | 60,3 | 191 | 16 | 99 |
| 1897 | 0,90 | 2,86 | 19,9 | 39,4 | 60,4 | 215 | 18 | 112 |
| 1899 | 1,03 | 3,88 | 21,5 | 42,0 | 71,6 | 259 | 22 | 163 |
| 1900 | 1,18 | 4,44 | 20,4 | 38,3 | 76,5 | 253 | 24 | 170 |
| 1901 | 1,22 | 5,13 | 21,8 | 40,6 | 20,5 | 291 | 27 | 208 |
| 1902 | 1,25 | 5,40 | 21,6 | 40,5 | 85,7 | 287 | 27 | 219 |
| 1903 | 1,39 | 5,73 | 20,9 | 39,7 | 82,6 | 310 | 29 | 227 |
| 1904 | 1,36 | 5,77 | 20,4 | 39,6 | 82,6 | 310 | 28 | 228 |
| 1905 | 1,45 | 6,54 | 21,6 | 42,7 | 87,7 | 355 | 31 | 279 |
| 1906 | 1,58 | 6,81 | 21,5 | 46,3 | 93,2 | 375 | 34 | 315 |
| 1907 | 1,63 | 7,13 | 21,3 | 45,3 | 93,2 | 384 | 35 | 323 |
| 1908 | 1,62 | 6,57 | 19,7 | 44,8 | 90,3 | 361 | 32 | 294 |
| 1909 | 1,62 | 6,68 | 21,1 | 52,8 | 100 | 387 | 34 | 353 |
| 1910 | 1,69 | 7,23 | 21,0 | 52,7 | 104 | 399 | 34 | 381 |
| 1911 | 1,69 | 7,78 | 21,0 | 49,9 | 102,2 | 412 | 34 | 388 |
| 1912 | 1,71 | 8,17 | 22,0 | 53,4 | 195,3 | 455 | 38 | 436 |
Принимая во внимание расчетные значения с и m из (3.6 и 3.7), получаем зависимости, позволяющие исключить величину с из расчетов P , T , c, т.е. имеем для с = const:
P = 22,213c –0,6307= 22,213( MV / Mў Vў ) –0,6307; (3.8)
T = 22,213c –1,2614= 22,213( MV / Mў Vў ) –1,2614; (3.8ў )
P = Tc 0,6307. (3.9)
Пусть в отличие от величины с величина с 2есть сечение константы скорости конверсии технологии в экономику, тогда из (3.6), (3.7) имеем:
с 2= PTc 1,8921, (3.10)
откуда следует, что PT , а также и P , и T есть фактически операторы, понижающие порядок m относительного обращения ценностей c . И поэтому можно записать:
inv = с 2= Tc +1,261; (3.11)
inv є с 2= Pc +0,6307(3.11ў )
Финансово-экономические операторы P , T , PT переводят относительную величину обращения ценностей в уровень технологии, определяемый константой скорости с или ее сечением с 2. Относительная ошибка в определении P , T по полученным данным для постоянных с и m не превышает 16%, что свидетельствует в пользу новой формы (3.6) – (3.11) финансово-экономического отношения между величинами P , T , MV , Mў Vў, которое до сих пор рассматривалось как чисто линейное (см. отношение (3.4)).
Полученный результат (3.6) – (3.11) позволяет утверждать, что между величинами P , T , c, уравнением состояния экономики h = h ( P , T , c ) и технологией n существует прямая аналогия [44] с электрической цепью типа треугольника или звезды. При этом в последнем случае векторы P , T , c имеют общую точку пересечения в основании координат n.
Будем полагать, что законы (3.6) – (3.11) есть пример отражения конкретного «способа выживания» экономики путем возникновения взаимно-однозначного соответствия между финансово-экономическими параметрами P , T , MV , Mў Vў, приведенными в экспериментальной табл. 3.1. Возникает вопрос: если данные табл. 3.1 — результат такого «выживания» по законам (3.6) – (3.11), то какова экспериментальная функция распределения j, например уровня цен P , и какой теоретической функции F отвечает такое распределение? Анализ величин j методом [43] показывает, что такая функция не есть нормальный закон, а j хорошо описывается логнормальным распределением (3.12) и с критерием Пирсона 1,98 в однопараметрической задаче (3.12ў ) соответствует реализации логнормального закона с вероятностью не менее 76% (табл. 3.2):
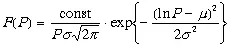 , (3.12)
, (3.12)
где const = 11,938; P — уровень цен (табл. 3.2); m = ln P ср.— логарифм среднего уровня цен P ; s — логарифм средней погрешности измерения s 2уровня цен P в табл. 3.2: s = ln s 2= 2,64.
Читать дальшеИнтервал:
Закладка:


![Сергей Кутолин - Зяма Пешков - легионер и бригадный генерал [рефлексия жизнеописания]](/books/1089689/sergej-kutolin-zyama-peshkov.webp)
