Вячеслав Кириллов - Логика: учебник для юридических вузов

В консеквенте ( S) предусмотрена сложная санкция: мошенничество «наказывается лишением свободы на срок до двух лет ( S 1 ) со штрафом до... ( S 2 ) или исправительными работами на срок до двух лет ( S 3 )». Связь между составными частями консеквента имеет следующий вид: S 1и S 2или S 3, или символически ((S 1 ∧ S 2 ) ∨ S 3 ). Логический анализ текста показывает, что такое истолкование является единственно возможным.

Если первоначальное условное суждение D → Sдетализировать в соответствии с проведенным анализом, то статья о мошенничестве представляется в следующей форме:

((d 1 ∨ d 2 ) ∧ (d 3 ∨ d 4 )) → ((S 1 ∧ S 2 ) ∨ S 3 ).

Главным знаком этого сложного суждения является импликация: антецедент суждения представляет собой конъюнкцию, оба члена которой — дизъюнктивные выражения; консеквент суждения — дизъюнктивное выражение, один из членов которого — конъюнкция из двух членов.

Овладение навыками логического анализа сложных высказываний с использованием символического языка для уяснения смысла правовых контекстов является эффективным средством точного истолкования и правильного применения норм в правовом процессе.

1. Какие суждения являются комбинированными сложными суждениями?

2. Какую роль выполняет логический анализ для точного толкования и правильного применения норм в правовом процессе?

Сложные суждения, как и простые, могут быть сравнимыми и несравнимыми.

Несравнимые — это суждения, которые не имеют общих пропозициональных переменных (простых суждений). Например, р ∧ qи m ∧ n.

Сравнимые — это суждения, имеющие одинаковые препозиционные переменные (простые суждения) и различающиеся логическими связками, включая отрицание. Например, сравнимыми являются два суждения: «Норвегия или Швеция имеют выход в Балтийское море» ( р ∨ q); «Ни Норвегия, ни Швеция не имеют выхода в Балтийское море» (˥ р ∧ ˥q). Хотя эти суждения различны по логической форме (первое из них — дизъюнктивное суждение, а второе — конъюнкция отрицаний, вместе с тем они сравнимы, поскольку включают одинаковые составляющие (простых суждений) ( ри q). Сравнимы следующие пары суждений: 1) р → qи ˥р ∨ q; 2) ˥r ∧ sи ˥(r ∧ s); 3) ˥m ∧ ˥nи ˥(m ∧ n). Наличие в каждой паре общих переменных позволяет сопоставлять их по смыслу и устанавливать истинность отношения.

Сложные сравнимые суждения могут быть совместимыми и несовместимыми.

К совместимым относятся такие сравнимые суждения, которые одновременно могут быть истинными. В сложных суждениях, как и в простых, различают три вида совместимости: эквивалентность, частичная совместимость и подчинение.

1. Эквивалентные — это суждения, которые принимают одни и те же значения, т. е. одновременно являются либо истинными, либо ложными.

В таблице 8 показано эквивалентное отношение между сложными суждениями. А и В — схемы суждений; знак ≡ — отношение эквивалентности для сложных суждений.

Таблица 8

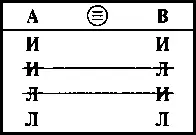
Таблица 9

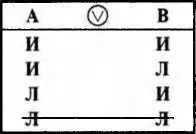
Таблица 10

1-я и 4-я строки таблицы показывают, что Аи Водновременно принимают одинаковые значения — Ии Л; зачеркнутые 2-я и 3-я строки показывают, что эквивалентные суждения одновременно не могут принимать различные значения.

Отношение эквивалентности позволяет выражать одни сложные суждения через другие — конъюнкцию через дизъюнкцию или импликацию и наоборот. Приведем четыре известные эквивалентности, которые являются законами логики.

1) Выражение конъюнкции через дизъюнкцию:

˥(A ∧ B) ≡ ˥A ∨ ˥B

2) Выражение дизъюнкции через конъюнкцию:

˥(A ∨ B) ≡ ˥A ∧ ˥B

Эти две эквивалентности называются законами де Моргана.

3) Выражение импликации через конъюнкцию:

˥(A → B) ≡ (A ∧ ˥B)

4) Выражение импликации через дизъюнкцию:

A → B ≡ ˥A ∨ B

2. Частичная совместимость характерна для суждений, которые могут быть одновременно истинными, но не могут быть одновременно ложными.

Отношение частичной совместимости для сложных суждений показано в таблице 9, где Аи В— схемы сложных суждений; ∨— знак частичной совместимости. 1-я строка таблицы говорит об одновременной истинности Аи В; 2-я и 3-я — несовпадение значений; 4-я строка зачеркнута, поскольку исключается одновременная ложность Аи В.

3. Подчинение между суждениями имеет место в том случае, когда при истинности подчиняющего подчиненное всегда будет истинным.

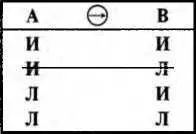
В таблице 10 показано отношение подчинения между сложными суждениями: Аи В— схемы суждений; → — знак подчинения. 1-я строка показывает, что в случае истинности Аистинным является и В. В 3-й и 4-й строках Аявляется ложным, а Впринимает произвольные значения. 2-я строка в таблице зачеркнута, поскольку отношение подчинения исключает ложность подчиненного Впри истинности подчиняющего А.

Отношение логического подчинения, позволяющее по истинности подчиняющего суждения определить истинность подчиненного, составляет основу фундаментального в науке логики понятия логического следования, регулирующею все виды рассуждений.

Несовместимыми являются суждения, которые одновременно не могут быть истинными. Это противоположность и противоречие.

1. Противоположность — отношение между суждениями, которые одновременно не могут быть истинными, но могут быть одновременно ложными.

В таблице 11 показано отношение противоположности между суждениями: Аи В— схемы суждений; ∧ — знак логической противоположности. 1-я строка таблицы зачеркнута. Это означает, что оба суждения одновременно не могут быть истинными; 2-я и 3-я строки показывают, что суждения могут принимать исключающие значения; 4-я строка — оба суждения могут быть ложными. Это значит, что при ложности одного из противоположных суждений нельзя установить значения другого: оно может быть как истинным, так и ложным.