Carlos Casado - Вначале была аксиома. Гильберт. Основания математики

∂²u/∂t² = c²∆u .

В свою очередь, уравнение тепла, которое регулирует распространение тепла (то, как оно движется из зон, где температура выше, в зоны, где она ниже), соответствует следующему виду:

∂u/∂t = k∆u .

Оба уравнения кажутся обманчиво похожими, за исключением того, что в первом вместо первой производной появляется вторая производная относительно времени. Эта тонкая математическая разница имеет чрезвычайное значение для физики: уравнение волн обратимо — в том смысле, что оно остается неизменным, если мы изменим направление течения времени. Математически: если мы заменим t на -t, уравнение останется прежним, поскольку при двойном дифференцировании знаки отрицания взаимно уничтожаются. Следовательно, уравнение не упорядочивает решения с течением времени, в связи с чем можно восстановить информацию о прошлом (по этой причине мы используем световые или звуковые сигналы для общения). Уравнение тепла, наоборот, необратимо (если заменить t на -t, мы не получим то же самое уравнение). Распространение тепла ориентировано темпорально, оно зависит от оси времени. Эта необратимость проявляется в том, что уравнение упорядочивает решения стечением времени, поэтому обычно невозможно восстановить информацию о прошлом (решение, соответствующее пику тепла, в итоге смягчается таким образом, что через некоторое время невозможно узнать, где и как возник взрыв или пожар, поскольку тепло распространилось по всему пространству).

Одной из проблем уравнения Лапласа, которая не давала покоя математикам и физикам XIX века, была так называемая проблема Дирихле, названная в честь немецкого математика Петера Густава Лежёна Дирихле (1805-1859). Она состояла в том, чтобы найти гармоническую функцию в области пространства, то есть функцию u, удовлетворяющую уравнению Лапласа Δu = 0 в этой области пространства, при этом на границе области (см. рисунок 1) она принимает заданные значения (например, u = ƒ на границе). То есть если обозначить область как Ω и границу области как γ,

Δu = 0 в Ω

u = ƒ в γ

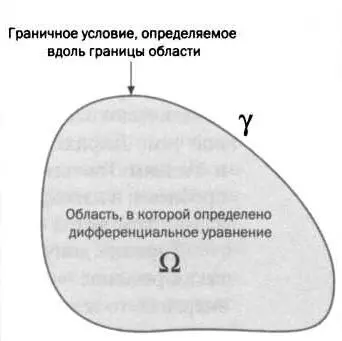
РИС. 1

В проблеме Дирихле ищут функцию и, которая принимает определенные значения на границе, и лапласиан, которой равен нулю внутри области.

Эта математическая проблема была связана со множеством физических проблем. Одна из них заключалась в ее решении. Представим себе упругую мембрану, равномерно растянутую над областью плоскости Ω, ограниченную кривой γ. Теперь предположим, что контур деформируется так, что каждая точка γ занимает некоторый уровень, заданный функцией ƒ. Естественно, вследствие деформации контура мембрана изогнется и начнет колебаться. Если позволить ей свободно колебаться, по истечении некоторого времени она достигнет равновесия, приняв некоторое положение (см. рисунок 2). Требуется вычислить величину деформации каждой точки внутри мембраны относительно плоскости, то есть высоту, которую сейчас занимает то, что переместилось. Функция u(х, у), измеряющая эти величины, соответствует проблеме Дирихле (в двух измерениях).

С точки зрения физики должна существовать функция u, являющаяся решением проблемы, кроме того, она должна быть единственной, поскольку рано или поздно мембрана остановится, и произойдет это единственным способом. Однако математически вопрос не настолько очевиден. В лекциях по данной теме Дирихле — как и Гаусс, Джордж Грин (1793-1841) и Уильям Томсон (1824-1907) — разработал метод решения проблемы и нахождения неизвестной функции и. Риман позже назвал этот метод принципом Дирихле.

Дирихле допустил, что в положении стабильного равновесия решение — функция u — должно обладать наименьшей энергией, то есть давать наименьшее значение для следующего интеграла {энергия Дирихле):

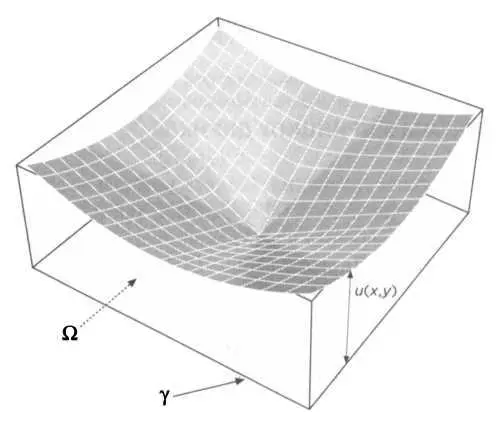
РИС. 2

Возможное положение равновесия мембраны через некоторое время.

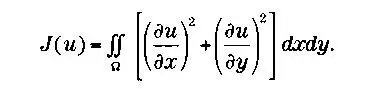
Другими словами, функция, которую мы ищем, должна давать — в сравнении со всеми возможными функциями, определяющими то же самое граничное условие, — наименьшее возможное значение для энергии. На физических основаниях оказывается возможным, что при любой заданной замкнутой кривой в пространстве существует поверхность с наименьшей энергией, которая ее заполняет, поскольку любая поверхность или мембрана будет стремиться принять конфигурацию, требующую наименьшей энергии.

Так как интегрируемое J(u) всегда положительно (является суммой квадратов), интеграл J(u) всегда больше или равен нулю. Поэтому Дирихле показалось рациональным, что должна существовать функция u, которая имела бы наименьшее значение. Заметьте, что если бы не было этой нижней границы, предполагающей нуль, могло бы оказаться так, что получаемые значения с каждым разом становились бы все меньше (0, -1, -2, -3...), причем это необязательно должно быть наименьшее значение. Предполагая существование этой минимизирующей функции u из J(u)> Дирихле доказал, что функция u гармоническая и, следовательно, удовлетворяет исходной проблеме, которую нужно решить.

Но оставалось неясно, действительно ли существует этот минимум, эта функция u, в которой интеграл Дирихле достигал бы своего наименьшего значения. Стоит подумать, например, о множестве всех действительных положительных чисел: они все больше или равны нулю, но нет ни одного, которое было бы наименьшим (для любого выбранного нами числа всегда будет меньшее число). Нижней границы множества (нуля) невозможно достичь в рамках самого множества (положительных чисел), так что нет и минимума. Усилия Вейерштрасса и его математической школы, направленные на строгое обоснование существования u, разбились об этот вопрос. Однако физики продолжали считать, что так называемый принцип Дирихле гарантирует решение проблемы Дирихле.

И лишь Гильберту — около 1904 года — удалось возродить принцип и доказать несомненное существование минимума. Но чтобы объяснить его доказательство, мы должны погрузиться в пограничную область вариационного исчисления, которое стремится определить, какие функции делают интеграл наименьшим.

Проблема брахистохроны, или кривой с самым быстрым спуском, исторически была первой проблемой в развитии вариационного исчисления. Среди всех кривых, соединяющих две точки, нужно найти ту, вдоль которой частица, двигаясь под действием силы тяжести, падает за меньшее время. При рассмотрении всех возможных кривых, соединяющих точку А с точкой В уищется минимизирующая время падения, что может быть выражено в виде интеграла. То есть ведется поиск кривой или функции, которая делает наименьшим значение этого интеграла. Данная проблема была предложена в 1696 году Иоганном Бернулли (1667-1748) и была решена независимо Ньютоном, Лейбницем, Иоганном и Якобом Бернулли. Решением оказалась не прямая линия и не дуга окружности, а дуга кривой под названием циклоида (см. рисунок 3).