Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

Это справедливо и для любого другого иррационального числа: мы всегда сможем приблизиться к нему через последовательность рациональных чисел. То же распространяется и на рациональные последовательности. Например, если мы возьмем число 0,75, то последовательность 0,751; 0,7501; 0,75001; 0,750001;... будет все ближе подходить к нему. То есть приближение любого вещественного числа возможно через последовательность рациональных чисел (что по сути и является решением Кантора задачи о континууме).

Математики XIX века, корпевшие над логическим обоснованием исчисления и открывшие ряды, то есть бесконечные суммы, выработали свои правила, которые существенно отличаются от тех, которые используются для привычных конечных сумм. В 1854 году немецкий математик Бернхард Риман (1826-1866) доказал: некоторые бесконечные суммы не обладают коммутативностью; другими словами, они могут быть реорганизованы так, что получится другой результат. Например, в ряде

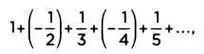
сумма которого равна 0,6931471..., слагаемые могут быть распределены так, чтобы получился любой желаемый результат.

Георг Фридрих Бернхард Риман, 1862 год.

Если Р — произвольное множество чисел, то производным от Р множеством Кантор называл группу чисел, которые можно аппроксимировать через последовательности, состоящие из элементов Р. Он обозначил такое множество Р. Если Q — множество рациональных чисел, то предыдущий пример показывает, что Q' = R, где R обозначает множество всех вещественных чисел.

Труды Кантора — прекрасный плод математического гения и одно из высочайших достижений человеческого интеллекта.

Давид Гильберт, немецкий математик

В статьях начала 1870-х годов Кантор представлял определение производного множества в терминах потенциально бесконечных множеств. Но сама структура Q' отсылает к актуальной бесконечности, поскольку Q заключает в себе все рациональные числа. С другой стороны, определение Q' приводит нас к последовательностям и к определению вещественных чисел. Рассмотрим теперь, как проблема тригонометрических рядов подтолкнула Кантора к двум основным темам его последующих математических исследований — к актуальной бесконечности и к задаче о континууме.

Теперь возьмем множество Р, состоящее исключительно из чисел 0, 1 и 2. Множество Р, по определению Кантора, содержит все числа, которые можно аппроксимировать посредством последовательностей, состоящих из бесконечных различающихся элементов Р. Очевидно, что бесконечных и различающихся элементов Р не существует, поскольку их в этом множестве всего три.

Так как создать даже одну последовательность элементов Р невозможно, то в Р ничего нет. В этом случае, как писал Кантор, Р аннулируется. Сегодня мы бы сказали, что Р — пустое множество, то есть в нем нет составляющих, но мы оставим выражение Кантора. Чтобы понять условие единственности, найденное Кантором, вернемся к примеру производного Q' и убедимся, что оно также является множеством чисел, а значит, мы можем рассчитать его производное. Кантор записывал производное от производного Q как Q". Поскольку оно тоже является множеством, то мы можем рассчитать и его производное, которое будет записано как Q (3); а его производное — как Q (4), и так далее.

В случае с Q эта цепь производных не дает интересного результата, потому что Q', Q", Q (3), Q (4),... являются множествами вещественных чисел, а значит, продолжая получать их производные, мы не достигнем ничего нового. Но существуют такие множества Р (о них мы не будем говорить подробно), производные которых Р', Р", Р (3), Р (4)... являются разными множествами или такими, что в конце концов процесс получения производных Р', Р", Р (3), Р (4)... аннулируется. Например, можно найти множество Р, для которого Р состоит из чисел 0, 1 и 2. В этом случае Р", производное от Р', аннулируется. В других случаях аннулируется Р' в третьих — Р (3)или Р (4)и так далее. Разумеется, для Q этот процесс никогда не закончится, потому что на всех его этапах мы получим множество вещественных чисел R. Условие единственности, найденное Кантором, состоит в следующем: если Р — множество абсцисс точек прерывания периодического графика, то для того чтобы был всего один способ разложить его в тригонометрический ряд, достаточно, чтобы процесс Р', Р", Р (3),Р (4),... рано или поздно заканчивался. Так Кантор смог ясно и точно изложить условие, обеспечивающее единственно возможный способ разложения на ряд Фурье, и решил задачу, поставленную перед ним Гейне в 1869 году.

Генрих Эдуард Гейне родился в Берлине, в Германии, 16 марта 1821 года и был восьмым из девяти детей. В 1838 году он поступил в Геттингенский университет и начал изучать математику, но в следующем году перешел в Берлинский университет, где 30 апреля 1842 года получил степень доктора. Два года спустя он стал преподавателем в университете в Бонне, а в 1856 году — в Галле. Там он читал различные лекции в разных областях вычисления и физики; его высоко ценили за ясность изложения. Гейне внес большой вклад в область логического обоснования вычисления. Он умер в Галле 21 октября 1881 года.

В 1860-е годы Гейне доказал, что способ разложения периодического графика будет единственным, если он непрерывен, а также если в каждом его периоде конечное количество «прерываний». Решение Кантора подходит для обоих результатов и для случаев бесконечного количества прерываний в каждом периоде.

То есть если наблюдается непрерывность, разложение будет единственным, если в каждом периоде конечное количество прерываний — результат будет тем же. Продолжая эти рассуждения, Кантор создавал гипотезы, которые звучали примерно так: «Если в каждом периоде есть бесконечное количество прерываний, но их «немного», то разложение будет единственным». «Бесконечные, но их немного» — эта фраза может показаться противоречивой, но не для Кантора. Для него «немногое бесконечное» означало «счетное бесконечное», то есть прерывания бесконечны, но их мощность при этом должна быть меньше мощности вещественных чисел.

Впечатление, которое производит на нас писанина Кантора, просто ужасно. Читать ее — настоящая пытка.

Шарль Эрмит, французский математик, 1883 год