Gustavo Pineiro - Бесчисленное поддается подсчету. Кантор. Бесконечность в математике.

В таком случае его называют периодическим. В XVIII веке математики обратили внимание на то, что очень многие физические явления — например, связанные с распространением звука или тепла — могут быть описаны при помощи периодических графиков. Они также заметили, что иногда эти графики оказываются прерывистыми, то есть в них наблюдаются резкие скачки. Например, на рисунке 3 представлен график, состоящий из последовательности косых линий. Чтобы изобразить его, мы должны отметить «скачок» от верхнего края каждой линии к нижнему краю следующей. Этот график описывает не физическое движение, а интенсивность звукового сигнала; горизонтальная линия обозначает нулевую интенсивность или тишину. Рассмотрим, как можно интерпретировать график при этих условиях. В начале — тишина, а затем появляется звуковой сигнал, который постепенно увеличивает интенсивность (это видно по тому, как возрастает первая косая линия); звук достигает своей максимальной интенсивности, а затем наступает тишина, но тут же опять начинает увеличиваться интенсивность звука, как в предыдущий раз, и снова достигает максимального уровня (мы видим, что вторая косая линия такая же, как первая). Опять наступает тишина, а затем повторяется та же схема, снова и снова.

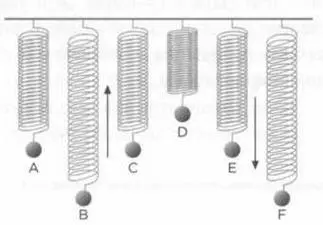
РИС.1

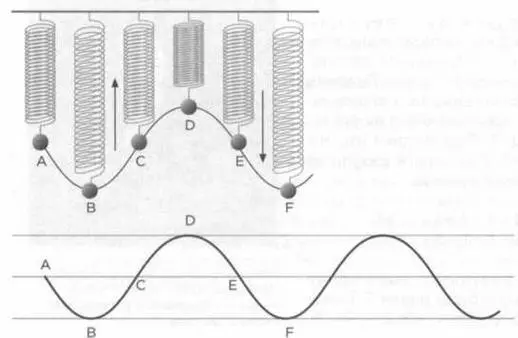
РИС. 2

РИС. 3

В начале XIX века французский математик Жозеф Фурье (1768-1830) разработал метод, который позволил ему записать любой график как сумму особых, при этом очень простых кривых, которые математически выражаются при помощи функций, названных тригонометрическими. Эти суммы, в свою очередь, обычно предполагают бесконечное (потенциально) количество кривых, и, так как в математике бесконечные суммы обычно называют рядами, этот метод сегодня известен как разложение на тригонометрические ряды, или ряды Фурье. Благодаря ему Фурье смог успешно изучить большое количество физических явлений, и он по-прежнему остается важным инструментом во многих областях математики, физики и инженерного дела.

Каков результат операции 1-1 + 1-1 + 1-..., которая продолжается бесконечно? Немецкий математик Готфрид Вильгельм фон Лейбниц (1646-1716) утверждал, что результатом этого «бесконечного вычисления» будет 1/2. Рассмотрим ход его рассуждений. Обозначим результат буквой S. Следовательно,

1-1 + 1-1 + 1-...=S

1-(1-1 + 1-1-...)=S.

Портрет Готфрида Вильгельма фон Лейбница, музей герцога Антона Ульриха в Брауншвейге (Германия), около 1700 года.

Поэтому результат выражения в скобках также будет равен S. Таким образом, получается, что 1 - S = S, откуда можно вывести, что S равно 1/2. Но мы можем сгруппировать члены выражения и по-другому:

1-1 + 1-1 + 1-.. . = (1-1)+(1-1)+(1-1)+... = 0 + 0 + 0+.. . = 0.

В этом случае мы получим 0. Или же мы можем сгруппировать так:

1-1 + 1-1 + 1-... = 1-(1-1)-(1-1)-... = 1-0-0-... = 1,

и результат будет равен 1. Какой же результат правильный: 1/2,0 или 1? Такие парадоксы мучили математиков на протяжении десятков лет, пока наконец в XIX веке не были выведены правила оперирования бесконечных сложений и вычитаний. На самом деле выражение 1-1+1-1+1-... не имеет никакого результата. Другими словами, предполагаемый результат на самом деле не существует. Рассуждения Лейбница неверны именно потому, что числа S нет.

В 1860-е годы в Галле Эдуард Гейне решил проверить, всегда ли будет одинаковым разложение такого периодического графика, как ряд Фурье. Другими словами, Гейне хотел узнать, может ли один периодический график быть записан в виде двух разных тригонометрических рядов.

Ему удалось доказать, что если в графике нет «скачков» или прерывностей, то он в самом деле будет иметь только один возможный вариант разложения. Но Гейне не нашел общего доказательства, которое было бы действительным для всех возможных ситуаций. Так, он не доказал единственность в случае, если в периоде — так называется классический постоянно повторяющийся график — бесконечное (потенциально) количество разрывов. Когда в 1869 году Кантор прибыл в Галле, Гейне предложил ему разобраться, будет ли разложение периодического графика всегда единственным, даже если количество «скачков» продолжит расти до бесконечности.

Кантор занялся этой задачей и в 1870 году получил первый результат: разложение будет единственным только при условии, что скачки распределены определенным образом, то есть отвечают особым требованиям. Точки графика имеют две координаты — абсциссу и ординату. Именно абсциссы должны выполнять эти условия. Однако Кантору было непросто выразить их конкретным, точным и изящным способом. Разумеется, он хорошо понимал, что это за условия, но не находил ясных и понятных слов для их описания.

С 1870 по 1872 год Кантор опубликовал пять статей, в которых окончательно сформулировал свое решение задачи единственного способа разложения ряда Фурье. В процессе помимо прочего он нашел ответ на проблему континуума, и поэтому его определение вещественных чисел через фундаментальные последовательности было опубликовано в рамках работы по тригонометрическим рядам.

Как же он смог сформулировать условие, которому должны соответствовать абсциссы прерывных точек периодического графика, чтобы их разложение на ряд Фурье было единственно возможным? Для этого Кантор разработал понятие производного множества, очень важное для нас, поскольку оно направило его на путь, который в итоге привел его к знаковой статье 1883 года. Рассмотрим, что такое производное множество и как с его помощью ученому удалось решить заданную Гейне задачу.

В нашем случае необходимо рассматривать последовательности, состоящие из бесконечного количества чисел, различных между собой.

Возьмем множество рациональных чисел. Очевидно, что π как иррациональное число не принадлежит к этой группе, и тем не менее его можно представить в виде последовательности рациональных чисел. Мы можем найти такую последовательность, состоящую исключительно из рациональных чисел, что по мере продвижения вперед будем получать числа все ближе к π. В примере из предыдущей главы последовательность 3,1; 3,14; 3,141; 3,1415;... получается путем прибавления к каждому последующему числу одного знака после запятой в числе π.