Знание-сила, 2005 № 03 (933)

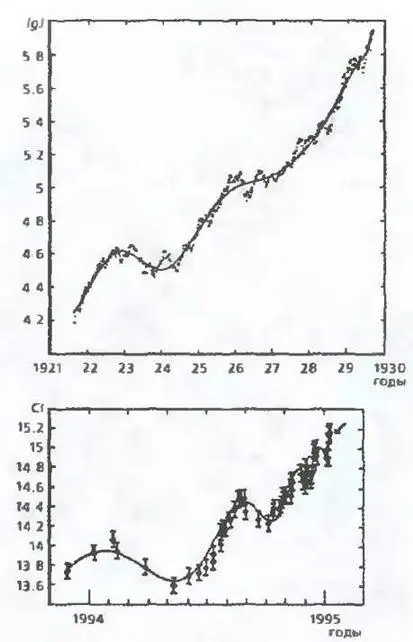
Рис.З

Сравните две кривые.

Сверху - зависимость логарифма индекса Доу-Джонса от времени перед Великой депрессией 1929 г. Внизу - зависимость концентрации ионов хлора в родниках перед землетрясением е Кобе в 1995 г.

И еще, пожалуй, одна картинка, показывающая, что самые разные катастрофические события могут развиваться по одним законам, — а это загадка и надежда на разгадку. Речь идет о сложно организованных иерархических системах.

На рис. 3 сверху по оси ординат отложен логарифм индекса Доу- Джонса, одного из главных индикаторов состояния экономики, по оси абсцисс — время вверху. Здесь показан период перед Великой депрессией 1929 года. Внизу — концентрация ионов хлора в родниках в период, предшествующий землетрясению в Кобе. Обе кривые очень похожи, обе описываются с высокой точностью одной формулой. И, видимо, за этим сходством кроется аналогия между механизмами обоих явлений, возможность перенести методы прогноза из одной области в другую. Возможно, это ключ к разгадке.

И еще одна задача. Допустим, мы живем в 1927 году и знаем, что ждет американцев через два года. Как уберечь людей от беды? Это проблема социума, направляемого развития, воздействия на общественное сознание.

Работа с информацией, основанная на компьютерных технологиях, глобальные телекоммуникации — сегодня главные козыри при управлении риском. Во-первых, потому, что каждая катастрофа должна учить. В XX веке у каждой катастрофы были "предтечи" — аварии того же типа, но меньшего масштаба. И чтобы предупредить "премьеру", надо на основе скромной "репетиции" менять нормы, планы, правила игры в социуме и техносфере. Лучше вложить тысячу в прогноз и предупреждение аварии, чем миллион в ликвидацию ее последствий. Во-вторых, информация и прогноз позволяют спасать тысячи жизней, сокращая время реагирования на события. В-третьих...

Впрочем, здесь надо остановиться. Работы, ведущиеся сейчас в Институте прикладной математики им. М. В. Келдыша РАН и в ряде академических институтов по инициативе Министерства по чрезвычайным ситуациям, показали, что здесь есть огромное поле деятельности, на котором Хаос занимает ключевое положение.

Природа, нем она ни будь,

Но черт ее соавтор —

Вот в нем суть.

И.В. Гёте. "Фауст"

Вернемся к динамическому хаосу. Спросим; если предсказывать даже с помощью современных компьютерных технологий так непросто, то как же нам удается ориентироваться в нашем сложном и быстро меняющемся мире? Как удается разумно действовать, несмотря на свой весьма скромный горизонт прогноза?

Сталкиваясь с различными задачами моделирования — от процессов лазерной термохимии и солнечного динамо до процессов исторических, — могу утверждать, что всех их объединяет необходимость находить параметры порядка в поведении сложных систем и составлять прогнозы.

Именно такой "тяжелой" системе и методам ее анализа и был посвящен грант РФФИ 97-01-00396, которым мне довелось руководить. Эта система описывает так называемую жесткую турбулентность — явление, при котором на хаотическом фоне иногда возникают гигантские всплески. Почему? Можно ли объяснить это на пальцах? Можно ли предвидеть "катастрофу"?

Принципиально важен вопрос; можно ли это явление, описываемое весьма сложной системой уравнений для бесконечного числа степеней свободы, смоделировать предельно просто? Если да, можно надеяться, что удастся удачно упростить и в других случаях. Если нет.., надо думать дальше.

Благодаря настойчивости и изобретательности С. В. Ершова и А. Б. Потапова был получен положительный ответ. Жесткую турбулентность удалось описать настолько просто, что численный анализ упрощенной системы сейчас можно поручить физтеху-второкурснику.

Однако вернемся к общему вопросу — как все же удается что-то предсказывать, несмотря на небольшой горизонт прогноза? Попытки получить на него ответ, а с ним и алгоритмы прогноза, предпринимаются в создаваемой сейчас теории русел и джокеров.

Одним из ее авторов по праву может считаться известный финансист Дж. Сорос. В своей "Алхимии финансов" он выдвинул идею "информационной", или "рефлексивной" экономики. В соответствии с ней такие переменные, как "уровень доверия", "ожидаемые прибыли" и многие другие, характеризующие нашу "виртуальную реальность", играют ключевую роль в современной экономике. Другими словами, в фазовом пространстве многих объектов, с которыми мы имеем дело в жизни, есть места, называемые областями джокеров, в которых случайность, не играющая никакой роли в другой ситуации, может оказаться решающей и не только повлиять на судьбу системы, но и скачком перевести ее в другую точку фазового пространства. Правило, по которому совершается этот скачок, и называется джокером. Название пришло из карточной игры. Джокер — карта, которой можно присвоить значение любой карты по желанию играющего. Понятно, что это резко увеличивает число вариантов и степень неопределенности.

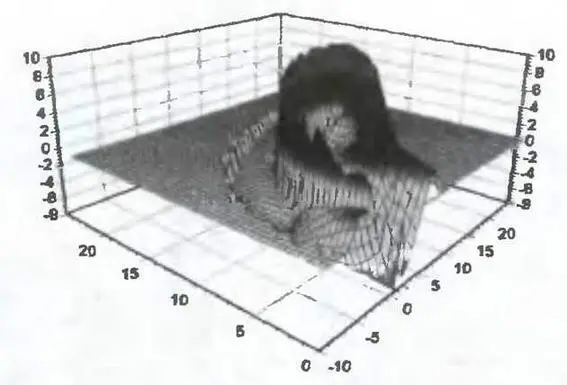
Рис. 4

Лекальные скорости разбегания (сходимости) для аттрактора Лоренца

С помощью представлений о джокерах можно говорить и о старых знакомых — динамических системах. Иллюстрацию этого придумал сотрудник нашего института И. В. Фельдштейн (рис. 4).

Речь опять идет о системе Лоренца. Скорость, с которой траектории разбегаются, лежит в области выше нулевого уровня, а скорость, соответствующая схождению, — в области ниже нулевого уровня. Видно, что область разбегания, которой естественно сопоставить джокер, довольно мала.

Но если нам не везет с прогнозами в области джокера, то где-то должно и везти. Подумаем: что значит "везет с прогнозом"? Это значит, что поведение системы с устраивающей нас точностью определяется лишь несколькими переменными, а обо всем остальном в первом приближении можно забыть. Кроме того, здесь должна быть возможность предсказывать на довольно большой срок. Такие области в фазовом пространстве и были названы руслами.

Вероятно, способность эффективно выделять русла, учиться не только методом проб и ошибок, совершенствуя свою предсказывающую систему и здравый смысл, и дала человеку решающее преимущество в ходе эволюции.

Но тут возникают вопросы: где начинается и где кончается русло? Какова структура нашего незнания? Как от одного информационного поля и одних представлений, адекватных этому руслу, переходить к другим, когда это русло кончилось? Знакомясь с разными экономическими, психологическими, биологическими теориями, трудно отделаться от ощущения, что, сами того не осознавая, их создатели имеют дело с разными реальностями, с разными руслами.