Алекс Беллос - Алекс в стране чисел. Необычайное путешествие в волшебный мир математики

Закон больших чисел утверждает, что если монету подбросить три раза, орел может не выпасть ни разу, но стоит подбросить ее три миллиарда раз, то наверняка выпадение орлов составит почти в точности 50 процентов. Во время Второй мировой войны математик Джон Керрик оказался в Дании. Немцы арестовали его и интернировали. Имея в своем распоряжении много свободного времени, он решил проверить закон больших чисел. Сидя в тюремной камере, он подбросил монетку 10 000 раз. Результат был таким: 5067 орлов, что составляет 50,67 процента от полного числа. Около 1900 года специалист по статистике Карл Пирсон проделал то же самое 24 000 раз. При заметно большем числе испытаний можно ожидать, что и процент будет ближе к 50 — и правда, у него выпало 12 012 орлов, то есть 50,05 процента.

Все эти результаты, по всей видимости, подтверждают то, что мы принимаем за само собой разумеющееся: если подбрасывать монету много раз, то орел и решетка выпадают с одинаковой вероятностью. Однако недавно группа исследователей из Стэнфордского университета во главе со специалистом по статистике Перси Диаконисом более глубоко исследовала этот вопрос — действительно ли эти события равновероятны. Для этого они соорудили машинку для подбрасывания монеты и провели замедленную съемку полета монеты по воздуху. Результаты анализа данных, полученных группой Диакониса — с учетом того, что монета может приземлиться на ребро примерно один раз за 6000 подбрасываний, — оказались захватывающе неожиданными: примерно в 51 проценте случаев монета падает на ту же сторону, с которой ее подбросили. Так что если в момент подбрасывания вверх смотрит орел, то орел будет выпадать немного чаще, чем решка. Диаконис заключил, впрочем, что его исследование на самом деле демонстрирует, насколько трудно изучать случайные явления, и что «для подбрасываемых монет классические предположения о независимости с вероятностью 1:2 достаточно твердо обоснованы».

Казино, без сомнения, имеют дело с большими числами. Как пояснил Бэрлокер, «вместо одной машины казино желают иметь тысячи, потому что они знают, что когда их много, то даже если одна какая-нибудь машина ведет себя неправильно, „наоборот“ — то есть проигрывает, — все равно для казино в целом имеется очень большая вероятность оказаться в плюсе». Игровые автоматы IGT сделаны так, что значение процента возврата поддерживается с точностью 0,5 процента после 10 миллионов проведенных игр. В «Перечнице», где я побывал во время моего посещения Рино, каждая машина разыгрывает около 2000 игр в день. При наличии почти 2000 машин получается около 4 миллионов игр за день. Так что уже через два с половиной дня хозяева «Перечницы» могут быть практически уверены, что значение процента возврата поддерживается с точностью в полпроцента. Если средняя ставка — доллар, а процент возврата равен 95 процентам, то за каждые 60 часов получается доход в 500 000 долларов, плюс-минус 50 000 долларов. Неудивительно, что хозяева казино так любят игровые автоматы.

Правила игры в рулетку не менялись со времен ее изобретения. Напротив, работа Бэрлокера нетривиальна отчасти и по той причине, что от него постоянно требуется придумывать новые расклады вероятностей всякий раз, когда его компания выпускает новый игровой автомат. Сначала он решает, какие символы использовать на барабане. Традиционно это вишни и надпись «bar», но в наши дни это вполне могут быть персонажи мультфильмов, художники эпохи Возрождения или животные. Далее он прикидывает, как часто эти символы будут встречаться на барабане, какие комбинации будут означать выигрыш и сколько машина будет платить за каждую выигрышную комбинацию.

Бэрлокер набросал для меня простенькую игру, описываемую ниже как Игра А — в ней имеются три барабана, на каждом из них 82 положения: вишни, bar’ы, красные семерки, джекпот и пустое место. Изучив таблицу, вы увидите, что имеется вероятность 9/ 82, или 10,976 процента, выпадения вишни на первом барабане, и в этом случае ставка в 1 доллар приносит выигрыш в 4 доллара. Вероятность выигрывающей комбинации, умноженная на выплату, называется ожидаемым вкладом . Ожидаемый вклад от комбинации вишни — любое — любое составляет 10,967 × 4 = 43,902 процента. Другими словами, на каждый доллар, опущенный в машину, 43,902 цента будет выплачено за комбинацию вишни — любое — любое. Проектируя игры, Бэрлокер должен обеспечить, чтобы сумма ожидаемых вкладов по всем выплатам равнялась установленному проценту возврата для автомата в целом.

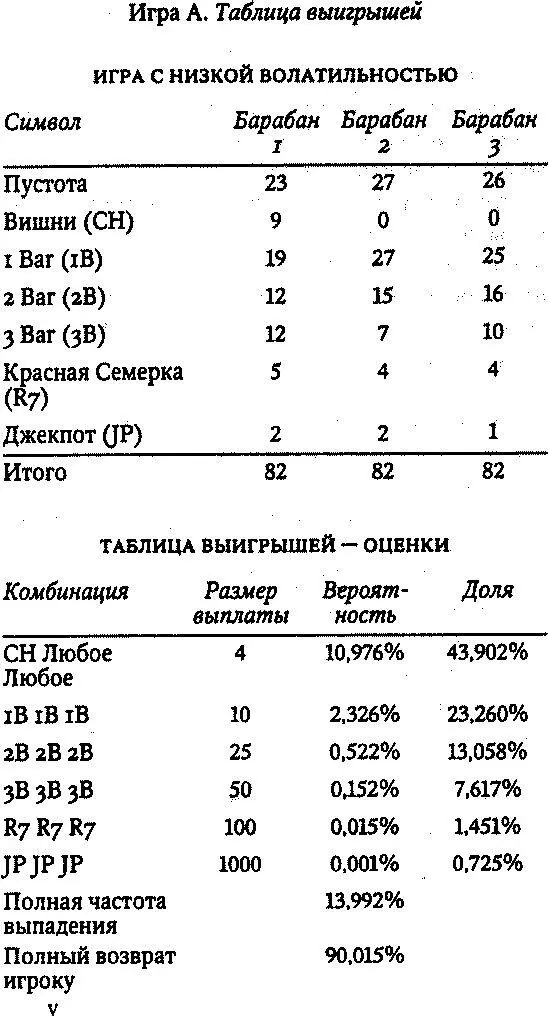
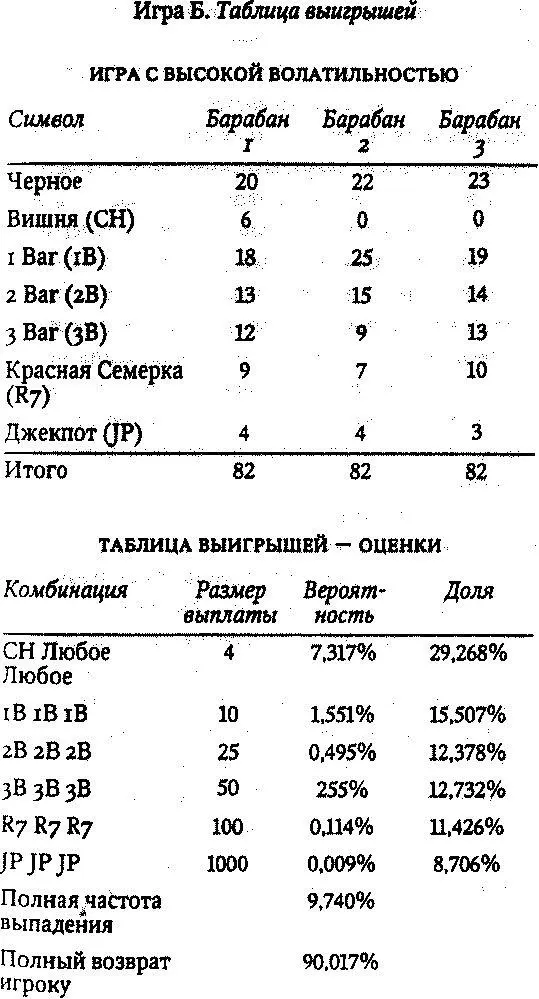
Гибкость в проектировании игрового автомата означает, что за счет варьирования используемых символов, выигрышных комбинаций и установленных выплат можно получать очень различные игры. Игра А — это «дриблинг на вишне», сие означает, что машина платит часто, но помалу. Почти половина всех выплачиваемых денег приходится на суммы всего в 4 доллара. Наоборот, в Игре Б только треть выигрышей приходится на выплаты в 4 доллара, тогда как гораздо большая часть денег отведена на более крупные выигрыши. Игра А — это так называемая игра с низкой волатильностью, а Игра Б — с высокой волатильностью; в ней вы будете попадать на выигрышные комбинации не так часто, зато растут шансы на больший выигрыш. Чем больше волатильность, тем выше риск для владельца игрового автомата на коротких отрезках времени.

Некоторые игроки предпочитают игровые автоматы с низкой волатильностью, тогда как другие — с высокой. Основная задача проектировщика игр — обеспечить достаточные выплаты для того, чтобы поддерживать в играющем желание продолжать игру, ведь чем дольше данный игрок играет, тем больше он в среднем проигрывает. Игры с высокой волатильностью вызывают большой азарт — особенно в казино, где машины, на которых выпал джекпот, привлекают всеобщее внимание, разражаясь вызывающими мурашки трезвоном и вспышками света. Однако создание хорошей игры не ограничивается разработкой изощренных графических элементов, насыщенных звуков и завлекательных видеороликов. Хорошая игра предполагает еще и создание правильного баланса вероятностей. Я спросил Бэрлокера, можно ли, по-разному настраивая волатильность, придумать машину с низким процентом возврата, которая для игроков была бы более привлекательной, чем машины с высоким возвратом.

— Мы с коллегами провели больше года, пытаясь в этом разобраться и выписывая всякие формулы, и нам удалось придумать метод, позволяющий скрывать, каков же в машине настоящий процент возврата, — сказал он. — Из некоторых казино до нас теперь доходят сведения, что там запускают машины с более низким процентом возврата, но игроки не вполне это осознают. То была непростая задача.