Ричард Бендлер - Большая энциклопедия НЛП. Структура магии [litres]

Формальные системы включают три компонента: [55] Более полно эти вопросы обсуждаются в любом вводном курсе логики; см., например: Tarsky (1943), Kripke (1972).

• словарь;

• набор аксиом;

• набор правил формирования, или вывода.

Наиболее важные (для наших целей) понятия формальной системы можно продемонстрировать на примере следующей системы, назовем ее «Простая». [56] Потому что такая она и есть.

Символ _ означает, что символы, находящиеся слева от него, могут быть замещены (быть переписаны как) символами, находящимися справа от него.

Теперь давайте посмотрим, как действует эта система. Метаправило (правило для правил) формальных систем данного класса требует, чтобы мы обосновывали каждое утверждение, которое делаем внутри системы. Есть два возможных способа обоснования: либо на основе того, что мы ранее заявили как аксиому, либо на основе подстановки, совершаемой в предыдущей строке в соответствии с правилами вывода. Поскольку у нас еще нет ни одной строки, в первой мы должны написать аксиому системы.

Теперь исследуем только что написанную строку и проверим, нет ли в ней символов, соответствующих левой части одного из правил вывода. В ней находится единственный символ , и этот символ действительно появляется в левой части обоих правил вывода системы «Простая». Теперь мы можем выбрать одно из правил и написать следующую строку.

Мы можем повторить процедуру, проверив, нет ли в последней строке символов, которые содержатся в левой части одного из правил вывода. Внутри нашей системы эта процедура может повторяться сколь угодно долго до тех пор, пока мы выбираем правило вывода а. [57] Система «Глубинная» Словарь: S (предложение), NP (именное словосочетание), VP (глагольное словосочетание), N (имя: существительное, местоимение), \/(глагол), Det (определение), РР (предложное словосочетание), Prep (предлог). Аксиома: S. Правила вывода: (a)S^NP VP N (в) VP -> V (NP) (г) РР -» Prep NP где символы внутри круглых скобок могут быть опущены, а символы внутри фигурных скобок означают альтернативный выбор, то есть можно выбрать либо одну строку символов, либо другую, но не обе вместе.

Допустим, вы выбрали правило вывода а еще дважды.

Что произойдет, если мы теперь выберем правило б?

Если мы теперь проверим последнюю строку последовательности, мы не обнаружим в ней символов, которые встречались бы в левой части какого-либо из правил вывода, так что процедура подошла к концу. Результат данной процедуры – совокупность всех строк, от первой до последней, – называется выводом. Последняя строка вывода называется теоремой системы и считается доказанной для данной системы. Наконец, последовательность элементов, входящих в словарь системы, считается правильно сформированной, если она представляет собой доказанную теорему данной системы. Рассматривая систему в целом, мы можем видеть, что последовательность элементов будет считаться правильно сформированной (в рамках данной системы) только в том случае, если ее вывод осуществляется из аксиомы с помощью правил вывода, до тех пор пока не будет получена строка, не содержащая символов, которые встречались бы в левой части какого-либо из правил вывода, то есть теорема. Если мы возьмем всю совокупность теорем системы, мы получим множество правильно сформированных последовательностей элементов данной системы.

Теперь мы хотели бы более отчетливо пояснить параллели между системой «Простая» и системами естественного языка. Первая задача, которая стоит перед нами как лингвистами, это определить множество правильно сформированных последовательностей элементов системы естественного языка, для которого мы пытаемся сконструировать грамматику. Затем, используя «Простую» в качестве модели, мы попытаемся определить систему правил, которая позволила бы нам представить в виде теорем все последовательности слов данного языка, которые носители языка считают правильно сформированными. Если мы сделаем это, можно будет считать, что мы сумели решить вопрос принадлежности к множеству.

Давайте посмотрим, какой могла бы быть система правил естественного языка.

Метаправило данной системы совпадает с метаправилом предыдущей системы «Простая» – каждая строка вывода может либо представлять собой аксиому, либо должна быть выводима из предыдущей строки на основе правил вывода. Используя ту же процедуру что и в случае системы «Простая», получаем.

Перейти от выводов к репрезентации в виде дерева очень просто: надо вернуться к первой строке вывода и начать читать его последовательно, строка за строкой. В каждой строке, применяя одно из правил вывода, заменяем один символ на другой символ (символы), а остальные символы просто копируем из предыдущей строки. Эти символы не несут новой информации и, следовательно, являются избыточными. Мы ликвидируем избыточность, стирая, или удаляя, в каждой следующей строке вывода все символы, на которые не повлияло приложенное правило вывода. Если мы выполним данную операцию с несколькими первыми строками вывода, то получим следующую фигуру:

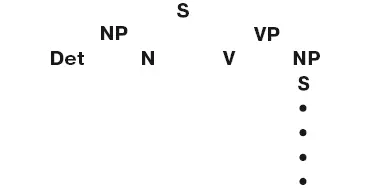
Теперь вернемся к первой строке вывода и, последовательно спускаясь вниз, соединим каждый символ из одной строки с тем символом или символами, на которые мы заменили их в последующей строке. В результате первые несколько строк приобретут вид

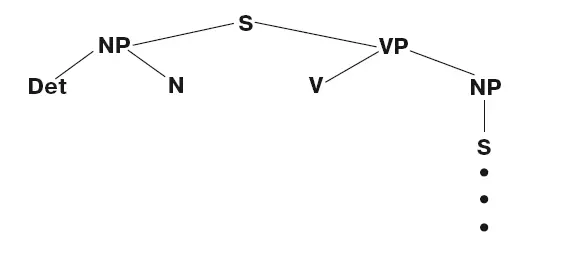
А когда мы применим эти две процедуры ко всему выводу целиком, мы получим репрезентацию в виде дерева.