Дэниел Левитин - Путеводитель по лжи [Критическое мышление в эпоху постправды]

средняя зарплата сотрудника: 66 тысяч долларов;

средняя зарплата владельцев: 100 тысяч долларов;

годовая прибыль на одного сотрудника: 42 тысячи долларов.

Теперь вы можете заявить, что 64 % зарплаты, которую вы выплачиваете своим сотрудникам (42 000 / 66 000), возвращаются к вам в виде прибыли, и это означает, что в итоге, получив прибыль, вы должны будете выплатить только 36 % их зарплат. Конечно, эти данные не свидетельствуют о том, что, наняв еще сотрудников, вы увеличите прибыль. Но в глазах того, кто не очень силен в критическом мышлении, это выглядит как весомый довод для увеличения штата.

А что, если вы хотите выглядеть невероятно честным и справедливым работодателем и показать, что разница между вашей прибылью и зарплатой ваших сотрудников довольно разумна? Возьмите прибыль в 210 тысяч долларов и разделите часть этой суммы, 150 тысяч долларов, в качестве бонуса между собой и своими партнерами. Об оставшихся 60 тысячах вы скажете позже, что это и есть «прибыль». На этот раз подсчитайте среднюю зарплату, включив в эти подсчеты себя и своих партнеров вместе с бонусами:

средняя зарплата: 97 500;

средняя прибыль владельцев компании: 20 тысяч.

А теперь повеселимся по-настоящему:

общие выплаты зарплат плюс бонусы: 840 тысяч;

зарплаты: 780 тысяч;

прибыль: 60 тысяч.

Теперь все выглядит разумно, правда? Из всей суммы в 840 тысяч долларов, включающей зарплату и прибыль, только 60 тысяч, или 7 %, составили личную прибыль владельцев. Ваши сотрудники будут думать, что вы безупречны, — кто станет обвинять владельца компании в том, что он присвоил 7 %? По сути, это ведь не так уж много: 7 % делится между владельцами компании поровну, и каждый получает по 2,3 %. Да тут даже возразить нечего!

А можно придумать и кое-что получше. Представьте, что в первый год существования вашей компании у вас были только сотрудники, работавшие неполный день. Они зарабатывали по 40 тысяч в год. На второй год у вас были только сотрудники, работавшие полный день. И они получали 66 тысяч, о которых говорилось выше. В таком случае вы со всей уверенностью можете заявить, что в среднем заработок каждого сотрудника увеличился на 65 %. Вы — великий предприниматель! Правда, вы замалчиваете тот факт, что сравниваете две несопоставимые вещи: работу на неполный и полный рабочие дни. Могу сказать, что в этом вы не первый: американская корпорация по производству стали U. S. Steel додумалась до этого еще в 1940-х годах.

В уголовном судопроизводстве то, как представлена информация, т. е. фрейминг {2} , оказывает сильное воздействие на мнение присяжных относительно виновности подсудимого. Хотя математически эти два утверждения эквивалентны [17], фраза: «Вероятность того, что обнаруженная на месте преступления кровь совпадет с кровью подозреваемого, если только это действительно не его кровь, составляет всего 0,1 %» (один к тысяче) гораздо убедительнее, чем заявление: «Кровь одного человека из каждой тысячи жителей Хьюстона тоже соответствует найденной».

Средние часто используют для того, чтобы рассказать о результатах, например «один брак из X случаев заканчивается разводом». Но это не означает, что статистика применима к вашей улице, к вашему бридж-клубу или к вашему знакомому. Брак либо закончится разводом, либо нет, но нужно знать определенные факторы уязвимости , чтобы предсказать, кто действительно разведется, а кто нет.

Еще один пример: вы можете прочитать, что один из пяти новорожденных детей — китаец. Вы подмечаете, что у шведского семейства, живущего на вашей улице, уже есть четверо детей, а сейчас они ждут пополнения. Но это не означает, что в семье родится маленький китаец. Среднее значение вычислено по всем рождениям в мире, а не в конкретной семье, в конкретном доме, в конкретном районе или даже стране.

Будьте осторожны со средними, а также с тем, как их интерпретируют. Один из способов ввести в заблуждение, используя средние, — усреднять данные по выборкам из несопоставимых совокупностей. Этот способ может привести к абсурдным выводам, как то:

В среднем у каждого человека одно яичко [18].

Этот пример наглядно показывает разницу между средним арифметическим, медианой и модой. Так как женщин в мире несколько больше, чем мужчин, медиана и мода будут равны нулю, в то время как среднее арифметическое будет близко к единице (возможно, оно будет равно 0,98 или около того).

Кроме этого, нужно быть внимательным и помнить, что среднее ничего не говорит о размахе значений. Средняя годовая температура в Долине Смерти в Калифорнии равна 25 °C, что считается комфортным. Но размах может быть просто убийственным, с колебанием температуры от –9 до 57 °C, — факт, зафиксированный приборами [19].

Или… Я мог бы вам сказать, что в среднем благосостояние сотни людей, находящихся в комнате, составляет колоссальную сумму: 350 миллионов долларов. Вы, наверное, думаете: вот бы отправить туда моих лучших менеджеров по продажам. Но в комнате могут находиться Марк Цукерберг (его состояние оценивается в 25 миллиардов долларов {3} ) и 99 бедняков. Таким образом, средний показатель может размыть разницу в важных показателях.

Если вы работаете со средними, остерегайтесь еще бимодального распределения . Вспомните, мода — это то значение, которое встречается чаще всего. Во многих наборах данных — биологических, физических, социальных — у распределения может быть два или больше пиков. А это значит, что два или больше показателей встречаются чаще других.

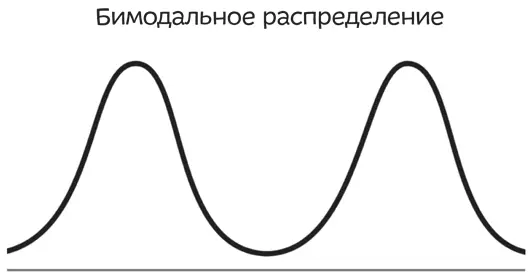
Например, подобный график может отображать сумму, потраченную на обеды в неделю (ось X ), и количество людей, потративших такую сумму (ось Y ) [20]. Представьте, что вы изучали две группы людей: детей (левый горб) — они покупают школьные обеды — и руководителей компаний (правый горб) — они ходят в дорогие рестораны. Среднее арифметическое и медиана в данном случае — это числа где-то между этими двумя горбами, и они ничего не скажут нам о том, что происходит на самом деле, — ведь во многих случаях среднее арифметическое и медиана отражают ту сумму, которую никто не тратит. Подобный график говорит лишь о том, что в вашем примере имеет место неоднородность — вы сравниваете яблоки с апельсинами. В таком случае лучше сразу сказать, что вы имеете дело с бимодальным распределением, и сообщить о двух модах. А еще лучше разделить группу на две подгруппы и собрать статистические данные для каждой.

Будьте осторожны, когда будете делать выводы об отдельных людях и о группах, основываясь на средних данных. Тут можно легко наткнуться на определенные подводные камни, которые даже получили собственные названия: «экологическая ошибка» и «ошибка исключения». Экологическая ошибка возникает, если мы делаем выводы об отдельном элементе, основываясь на совокупных данных (таких как средняя величина группы), а ошибка исключения — если делать все ровно наоборот.