Аркадий Егидес - Лабиринты мышления или учеными не рождаются

Надо всемерно стараться свести содержание к одному из четырех вариантов. В науках эта четверка наиболее значима.

Мы, правда, еще договорились о том, что отображать увеличение чего–либо будем так:

Уменьшение чего–либо — так:

А если в тексте указание только на временнуюпоследовательность, но ничего не говорится о характере этой последовательности, то — так:

Все это тоже можно применить по случаю, но такие случаи в науке встречаются существенно реже. Но вот «наша совесть чиста». Старались изо всех сил свести к «четверке» и даже найти возможность свести к дополнительной «тройке», но не получается, не судьба Такое возможно. Ну что ж, прибегнем, как мы уже договорились, к «свободной» записи.

* * *

Трудно бьшает соблюсти абсолютно все правила, о которых мы говорили в первых главках книги. Мы писали, что выноски должны быть вне поля схемы. Схема должна представлять соотношения понятий в чистом виде, без помех. А выноски мешают. Но вот что–то из выносок «заскочит» внутрь собственно схемы. Не уместилось. Если это как исключение, а не как правило, потерпим. Или, наоборот, что–то из смысловых структурных фигур «выскочит» за воображаемую рамку в «поле выносок», тоже как исключение, а не как правило, потерпим. Что–то непохожее не будет выделено цветом и формой рамки — что же, удовлетворимся лишь разницей в расположении. Но стремиться к максимальному соблюдению оговоренных правил все же надо. Примером исключения из правил может послужить все та же наша многосложная схема, иллюстрирующая фрагмент из «Комманифеста». Аббревиатуру «П НС СС» мы взяли в нескольких местах в прямоугольные рамки с углами. Так удобнее выделить и удобнее сделать выноски с расшифровками. А линий, параллельных прямоугольникам, вблизи нигде нет. Так что прямоугольники с углами здесь не только допустимы, но и целесообразны.

Обратим особое внимание, что сложные научные тексты требуют сложных логико–графических структур. Взглянем вновь на рис. 148, где «яйцо превращается в цыпленка под воздействием тепла курицы и генетических механизмов», и отфиксируем логико–графическую структуру, отображающую это. Схема простая, даже простенькая по сравнению с логико–графической структурой (рис. 160), отображающей фразу из «Комманифеста». Как говорится в рекламных роликах, почувствуйте разницу. Но как бы ни сложна была л огико–графическая структура, онадолжна быть хорошо гешгальтирована.Теперь, когда мы

имеем пример многосложной схемы («Комманифест»), убедимся, что в ней много простых логико–графических схем,каждая из которых более или менее хорошо вьщеляется как гештальт из фона, то есть из всей многосложной схемы. Для экономии места мы видоизменили каждую простую схему, но ее легко отыскать в большой схеме. Вот они — эти простые схемы. Их много (см. рис. 161).

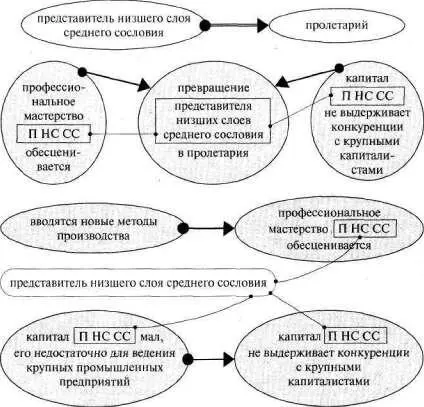
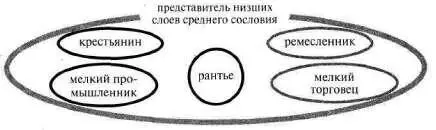
Рис. 161 (начало)

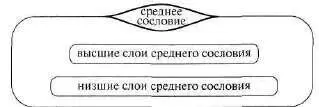
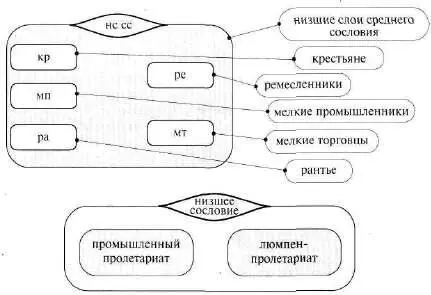
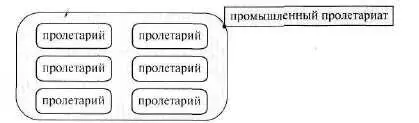
Рис. 161 (продолжение)

Встает вопрос: если многосложная схема состоит из простых схем, то, может быть, ее лучше и строить сразу от простого к сложному?

Действительно, вот мы видим новый текст, читаем, вдумываемся, выписываем из него все значимые понятия. Вспомним, что понятия могут выражаться одним словом, двумя, тремя, несколькими. А могут несколько понятий выражаться и одним словом. Так вот, мы выписываем все значимые понятия, в скольких бы словах они ни выражались. И подчеркнем, что выписываем именно ЗНАЧИМЫЕ понятия. Каждое из них обводим рамкой. Поначалу неважно какой. Далее решаем, как соотносится каждое понятие с каждым понятием.Ведь в многосложной схеме все равно это должно быть отражено. Если мы продумаем это тщательно, то будет построено достаточное число простыхили сложных одноплановыхсхем, которые затем можно будет соединить в сложные разноплановые.

Проверим, как это получится, все на той же многострадальной фразе из «Комманифеста». Выписываем следующие понятия (см. рис. 162).

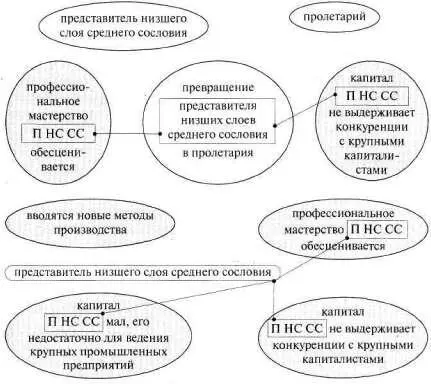
Рис. 162 (начало)

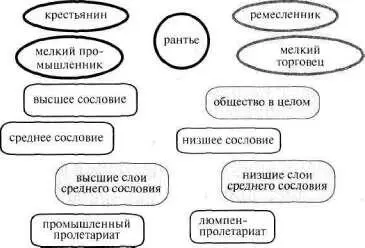
Рис. 162 (продолжение)

Выделив эти понятия, начинаем искать соотношение каждого с каждым.Повторим это: КАЖДОГО С КАЖДЫМ.Если это не перекрест и не включение, то, может бьпь, это внеположное соотношение. Или часть и целое. Или трансформация. Или причина–следствие. Или что–то не из «четверки». Алгоритм, больше–меньше, увеличение, уменьшение, простая последовательность событий, что–то другое дельное, что можно отобразить в свободной форме. Так мы получаем множество простых схем, каждая из которых объединяет всего два понятия.

А дальше соединяем простые схемы с «отдельно стоящими» понятиями и получаем сложную одноплановую или сложную двуплановую схему. Можно сделать сложную схему из двух простых. Сложные од–ноплановые и сложные двуплановые соединяем с отдельно стоящими понятиями или одной–двумя–тремя простыми схемами. Можно сложные схемы соединить со сложными же схемами, получая еще более сложные. И так далее.

А стоит ли делать все так последовательно и основательно? Ведь возможен и второй путь. Можно построить всю многосложную схему сразу и утолить свое самомнение, повысить самооценку и уровень притязаний. Если сразу получится что–то сделать сложное и многосложное — ради бога, делайте. Получится — хорошо. Не получится — и тогда не следует отказываться от построения схемы вообще, а стоит возвратиться на первый путь. И уж тогда обязательно перепроверить