Аркадий Егидес - Лабиринты мышления или учеными не рождаются

Рис 231

РЕШЕНИЕ ЗАДАЧИ 38, расположенной на с. 152. См. рис. 232.

Рис. 232

РЕШЕНИЕ ЗАДАЧИ 23, расположенной на с. 149. См. рис. 233.

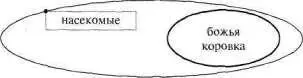
Рис. 233

РЕШЕНИЕ ЗАДАЧИ 12,

расположенной на с. 147.

«Наука об обществе» — это род. История — вид науки об обществе, отличающийся от других видов тем, что описывает его изменения во времени». Можно составить текст покороче, без указания на то, что род, что вид: «История — наука об обществе, описывающая его изменение во времени».

РЕШЕНИЕ ЗДЦАЧИ 49,

расположенной на с. 155.

Приготовьтесь, пожалуйста, к трудному разговору. Из этих шести треугольников получится много чего. И мнений–сомнений много.

Начнем с недоумения, почему Евклиду захотелось выделить именно по таким признакам треугольники. Это одним древнегреческим богам известно. Ведь можно было бы вьщелить еще г великое множество треугольников. Положим, треугольник с соотношением сторон 4,5,6. Это был бы вид тупоугольного треугольника, но ведь и египетский треугольник — вид прямоугольного. Можно вьщелить треугольник с одним углом в 30 градусов. Чем он хуже прямоугольного, у которого один из углов равен 90 градусов? Но что дано, то дано. Так развивалась мысль. Может быть, даже чисто случайно. А может быть, и закономерно… Мы уже говорили, что живем больше в прямоугольном мире. Так что середина для нас — прямоугольный треугольник, а тупоугольные и остроугольные — как бы отклонения от него. Но не в этом сейчас проблема. Евклидову геометрию изучают две с лишним тысячи лет. Так что давайте уж поймем соотношение тех треугольников, которые и выделены в школьном курсе вслед за Евклидом. Все–таки древний грек. Воспылаем к нему уважением и за это. Ладно, здесь мы не будем уяснять соотношение каждого с каждым, как мы это делали с четырехугольниками. Пойдем более быстрыми шагами. Но все же будем работать в духе наращивания схемы.

Итак, уясним соотношения остроугольного треугольника, прямоугольного треугольника и тупоугольного треугольника. Они радопо–ложны.Рисовать будем с расчетом на будущее. Этим обусловлена некомпактность первых рисунков. Но она работает на компактностьпоследующих рисунков. Читатель мог начать работу с компактных рисунков, и догадки, возможно, были затруднены, надо было потом видоизменять рисунки. А наши первые рисунки — экспликация из уже сложившейся сложной схемы. См. рис. 234.

А как каждый из этих треугольников соотносится с понятием «равнобедренный треугольник»? Поясним, что остроугольный треугольник может быть равнобедренным, но может и не бьпь равнобедренным. И равнобедренный треугольник может быть остроугольным, а может и не быть остроугольным. Так что соотношение тут перекрестное. Аналогично складывается соотношение понятий «равнобедренный прямоугольник» с понятием «прямоугольный треугольник» и с понятием «тупоугольный треугольник». Изобразим это все вместе так. См. рис. 235.

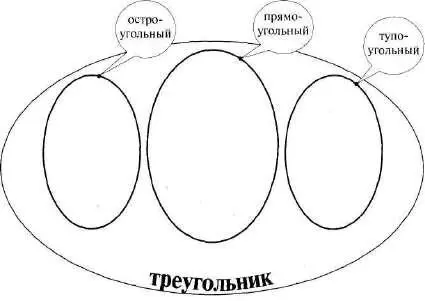
Рис. 234

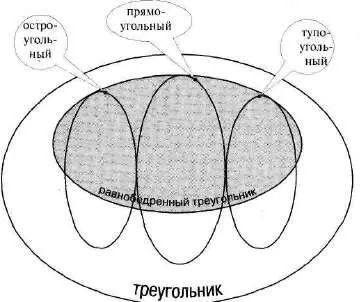
Рис. 235

Мы вынуждены ввести понятия, которые не фигурируют в школьном курсе геометрии. На перекрестьях расположились треугольники: «равнобедренный остроугольный», «равнобедренный прямоугольный», «равнобедренный тупоугольный». Внесем их в схему, взяв каждое из этих новых понятий в рамку. См. рис. 236.

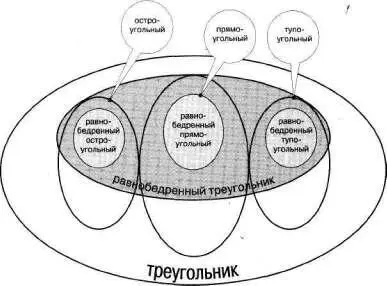
Рис. 236

Уясним теперь, каково место в этой классификации равностороннего треугольника. Припомним, в равностороннем треугольнике не только все стороны равны, но и все углы равны. При этом каждый угол вынужденно острый (60 градусов). Так что понятие «равносторонний треугольник» включаем в понятие «остроугольный треугольник». В другом плане: если у него все стороны равны, то и две любые стороны конечно же равны. А потому включаем понятие «равносторонний треугольник» в понятие «равнобедренный треугольник». И уточняем далее, что равносторонний треугольник является видом изобретенного нами «равнобедренного остроугольного треугольника». Название «равнобедренный остроугольный треугольник» превратим в аббревиатуру «р–б о–у», расшифровку которой дадим уже в выноске. Придется потесниться, ведь нужно место для аббревиатуры «р–ст», которая тоже расшифрована в выноске как «равносторон–ний». Но ведь есть треугольники «равнобедренные остроугольные, но не равносторонние». Мы вынуждены их вьщелить и обозначить в схеме аббревиатурой «р–б о–у неравн–ст»с расшифровкой в выноске. См. рис. 237.

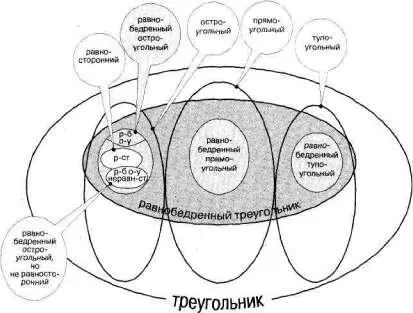
Рис. 237

Итак, мы нашли соотношение пяти исходных понятий (равнобедренный, равносторонний, остроугольный, прямоугольный, тупоугольный треугольники ) между собой и с четырьмя вынужденно выведенными. Имеются в виду «равнобедренный остроугольный», «равнобедренный прямоугольный», «равнобедренный тупоугольный», «равнобедренный остроугольный неравносторонний» треугольники. Но остается загадкой, в каком соотношении с ними со всеми, находится египетский треугольник. Для того чтобы ее разгадать, надо разобраться со всеми треугольниками, которые не являются равнобедренными. Или скажем иначе (и имеем на это логическое право), являются неравнобедренными.То есть мы должны ввести в лексикон новое понятие «неравнобедренный треугольник» и осознать, что неравнобедреннымитреугольниками являются некоторые остроугольные, некоторые прямоугольные и некоторые тупоугольные прямоугольны–ки. Можно сказать и так: остроугольный прямоугольник может быть равнобедренным(это мы уже нарисовали), но может быть и неравнобедренным (это еще нарисуем). Аналогично этому прямоугольный треугольник может быть равнобедренным и неравнобедренным. Итупоугольный треугольник бывает равнобедренным и неравнобедренным.Ну и, следовательно, мы вынуждены ввести три новьгх понятия:

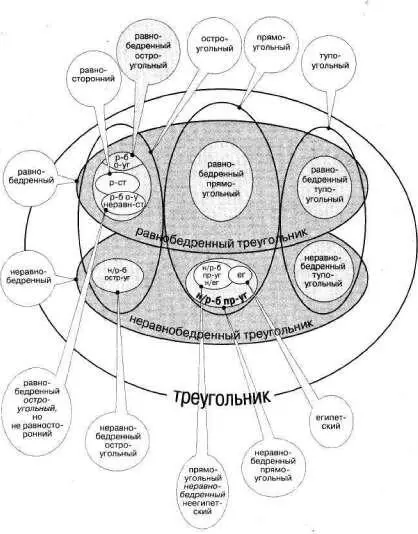
Рис. 238

• неравнобедренный остроугольный

• неравнобедренный прямоугольный