Аркадий Егидес - Лабиринты мышления или учеными не рождаются

Рис. 247

Живет яйцеклетка 6—12 часов, редко до суток.Самое позднее овуляция произойдет на 12–й день от конца. Так что последние 11 дней бесплодны.Это минимум. Но если овуляция произошла на 14–й день от конца, то, по этой логике, бесплодие в конце цикла длится 13 дней. Но самое раннее — овуляция может наступить на 16–й день от конца. Тогда бесплодие в конце цикла — 15 дней. Это максимум. См. рис. 248.

Рис. 248

Учесть, однако, надо не только то, сколько живет яйцеклетка, но и сколько живут сперматозоиды. Запомним и этот важный для наших рассуждений «параметр»: двое суток,но они могут прожить и трое суток. Это важно учесть до выхода яйцеклетки. Самое раннее — овуляция, напомним, бывает на 16–й день от конца цикла. Так что если сперматозоиды попадают на 17–й день от конца, на 18–й день от конца или даже на 19–й день от конца, то может состояться беременность. Значит, эти дни — 17–й, 18–й, 19–й от конца цикла — включим в «период вероятной плодности» — таков термин в отличие от бытового «опасные дни» (ведь они могут бьпь и желанные… если люди хотят ребенка). Итак, период вероятной плодности в целом длится с 12–го дня от конца по 19–й день от конца. Не забудем при этом пояснительное слово «включительно». См. рис. 249.

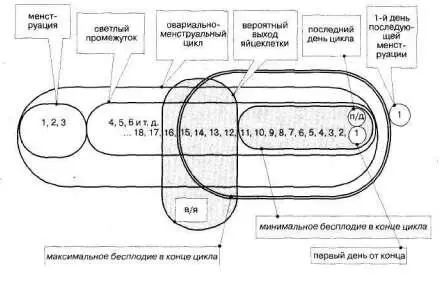
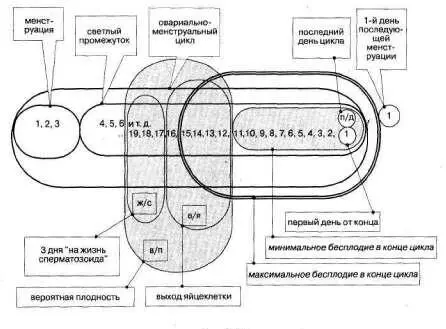
Рис. 249

Про бесплодие в конце цикла мы договорились: минимум 11, максимум 15. Но пока мы не знаем, когда же конкретно вышла яйцеклетка, будем считать по максимуму или по минимуму? Вопрос риторический. Конечно, по минимуму. Значит — 11 дней. Но сколько же бесплодных дней в начале цикла, до овуляции? Здесь не надо знать высшей математики, чтобы вывести простую формулу: «цикл минус 19». Если цикл 28 дней, то количество бесплодных дней в начале его — 9 (цикл минус 19 = 28–19 = 9)… См. рис. 250.

Вы обратили внимание, что части и целое здесь — в сложном переплетении. «Вероятная плодность» состоит из «вероятного выхода яйцеклетки» и «грех дней на жизнь сперматозоида». Цикл — из менструации и «светлого промежутка». Цикл делится на периоды вероятной плодности, бесплодия в начале цикла и бесплодия в конце цикла. Есть еще и максимальное бесплодие. Возможен вариант, когда вероятная плодность включает дни из «светлого промежутка» и менструации. Но этот «виртуальный» вариант в схему не вошел, просто мы называем и его для комплекта.

Схема не уместилась в горизонтальных пределах страницы, поэтому нам пришлось ее расположить иначе. Пользоваться ею в книге ста-

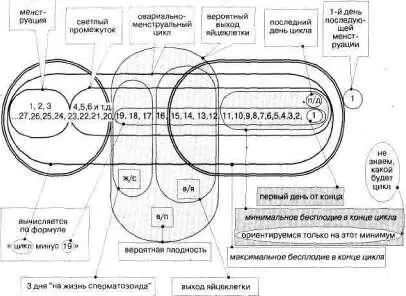
Рис. 250

ло труднее, но что делать? Впрочем, ведь ее можно скопировать и поместить горизонтально.

Восклицательный знак (!): мы составили очень сложную, но одно–плановую схему. Как и с треугольниками, только там план классификационный, а здесь части и целое.

Приведенные соотношения понятий настолько очевидно сложны, что практикующие врачи вообще игнорируют их в своем «санитарном просвещении». Да и в научных книгах эти соотношения изложены сложновато даже для специалистов. Нам удалось перевести книжные тексты в наши схемы благодаря нашей технологии. И наш опыт показывает, что такое изложение делает доступным этот сложный материал широкому кругу людей. Это — и по результатам наших занятий с народом, и по результатам издания книги «Лабиринты общения» (АСТ–ПРЕСС, 2002), где все приведено в таком же виде, как здесь.

РЕШЕНИЕ ЗАДАЧИ 13,

расположенной на с. 147. «Больной выздоровел».

РЕШЕНИЕ ЗАПАЧИ 34, расположенной на с. 152. См. рис. 251.

Рис. 251

РЕШЕНИЕ ЗАДАЧИ 19,

расположенной на с. 149. См. рис. 252.

Рис. 252

РЕШЕНИЕ ЗАДАЧИ 65,

расположенной на с. 212.

S Карточка 1

• Лицевая сторона.

Как описывается гиперкомпенсация по Альфреду Адлеру в коллективе школьников?

• Оборотная сторона.

Школьник гиперкомпенсирует за счет младшего свой комплекс неполноценности по отношению к старшему.

РЕШЕНИЕ ЗАДАЧИ 31,

расположенной на с. 151. См. рис. 253.

Рис. 253

РЕШЕНИЕ ЗАДАЧИ 54, расположенной на с. 159.

В тексте отсутствует информация о том, что мозговые пузыри развиваются из головного отдела нервной трубки. Скорее всего, это именно так. Но все же авторам надо было бы это сказать. А вдруг не из головного отдела… То, что здесь имеется в виду, по нашей терминологии — трансформация, видно сразу. Но у этого варианта трансформации есть особенности. Нервная пластинка превращается в нервную трубку, то есть одно в другое, а передний пузырь — в конечный мозг и в промежуточный мозг, то есть одно превращается не просто в другое, а это другое представляет собой два, а не одно.А задний пузырь превращается даже в три, ане в два:в мозжечок, в продолговатый мозг и в мост. Еще критика в адрес текста. В нервной трубке у авторов назван головной отдел и почему–то нет ни одного «неголовного» отдела. Это оставляем на их усмотрение. В логико–графической схеме мы это оставили в соответствии с авторским текстом. См. рис. 254.

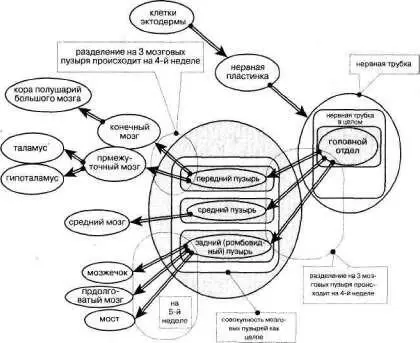
Рис. 254

Обратим внимание на то, что нервная трубка в нашей логико–графической схеме представлена в двух ипостасях. С одной стороны, нервная пластинка становится нервной трубкой, то есть одно превращается в другое (пластинка — в трубку). А с другой стороны, нервная трубка имеет головной отдел и (подразумевается) другие отделы. Значит, нервная трубка — целое. И есть ее части, одна из которых представляет собой головной отдел. Аналогично обстоят ' дела и с «мозговыми пузырями». Они — то «другое», во что превратился головной отдел нервной трубки. И в то же время они то целое, которое делится на три части: передний мозговой пузырь, средний мозговой пузырь и задний мозговой пузырь. Соответственно соотношения части и целое представлены смягченными прямоугольниками. А превращение в качественно иное «другое» отображено овалами и соответствующими трансформационными стрелками. Нервная пластинка в овале превращается («с помощью» стрелки) в нервную трубку. Внимание: при трансформации один род превращается в другой род.