Юрий Ревич - Занимательная электроника

Все сказанное относилось к случаю, когда мы измеряем одну величину, имеющую некоторую случайную погрешность. Однако на практике нам часто требуется по экспериментальным данным получить оценку некоторой функции у( х ) — фактически это задача построения кривой по результатам опытных данных, которую вам, несомненно, приходилось не раз решать, если вы обучались в техническом вузе.

Процесс проведения кривой через какие-либо точки (расчетные или экспериментальные) в общем случае называется аппроксимацией . Аппроксимацию следует отличать от интерполяции (когда по совокупности имеющихся значений функции и переменных рассчитывают значение функции в некоторой точке между ними) и экстраполяции (когда рассчитывают значения функции вне области, охваченной имеющимися значениями, в предположении, что там кривая ведет себя так же). Насчет последней операции следует отметить, что полиномы, полученные регрессионным способом (см. далее), за исключением разве что прямой линии, обычно для проведения экстраполяции не годятся — т. к. не несут в себе физического смысла и вне экспериментальной области могут очень сильно расходиться с реальной картиной.

Провести кривую, аппроксимирующую опытные данные, можно от руки на миллиметровке, но как решать такую задачу «правильно»? Причем, как и в предыдущем случае, желательно бы иметь возможность оценить погрешности измерений.

Принцип такого построения при наличии случайных ошибок измерения иллюстрирует рис. 13.7.

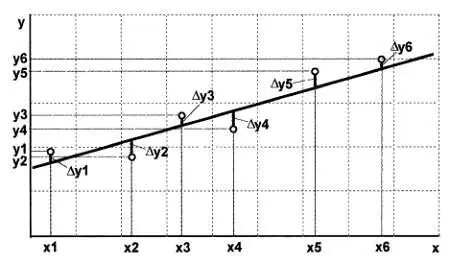
Рис. 13.7. Проведение аппроксимирующей прямой по экспериментальным данным

Разумно было бы проводить кривую (в данном случае — прямую) так, чтобы отклонения Δу i ,- были бы минимальными в каждой точке. Однако просто минимизировать сумму отклонений не получится — они имеют разный знак, и минимум получился бы при очень больших отрицательных отклонениях. Можно минимизировать сумму абсолютных значений отклонений, однако это неудобно по ряду чисто математических причин, потому используют уже знакомую нам сумму квадратов отклонений, — только ранее это было отклонение от среднего арифметического одной величины х , а теперь это отклонение опытных данных от кривой у( х ):

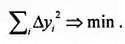
Такой метод называется методом наименьших квадратов .

Кстати, а какую именно кривую выбрать? Ведь кривые бывают разные: прямая, парабола, экспонента, синусоида… Опыт показывает, что на практике можно ограничиться полиномом, соответствующим разложению функции в ряд Тейлора (в математике доказывается, что любую другую непрерывную функцию всегда можно представить в виде такого ряда):

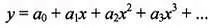
(5)

Это уравнение называется уравнением регрессии . Отметим, что здесь мы рассматриваем наипростейший случай — зависимость у от одного параметра x . В общем случае независимых переменных может быть несколько, но для наших целей простейшего случая достаточно. Еще отметим, что величины x i считаются неслучайными — если в каждой i -й точке проводится несколько измерений, то надо брать среднее. Случайными считаются только величины y .

Итак, в качестве исходных данных у нас имеется некий набор значений x i в количестве n штук. Надо провести кривую, соответствующую уравнению (5), так, чтобы сумма квадратов отклонений была минимальна:

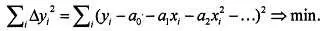
(6)

Какой степени полином должен быть? Из элементарной геометрии известно, что через две точки можно провести прямую (полином первой степени), через три — параболу (второй степени) и т. д., т. е. максимально возможная степень полинома на единицу меньше, чем число экспериментальных данных. Однако через две точки можно провести только одну прямую, и мы никогда не сможем оценить погрешностей — т. е. узнать, насколько наша прямая отличается от того, что имеет место в действительности. Поэтому чем избыток точек больше, тем лучше (в идеале необходимы те же 15–20 точек, но на практике для линейной зависимости можно обойтись и тремя-пятью точками). Оптимальную же степень определяют так: строят несколько полиномов разной степени и смотрят на среднеквадратическое отклонение. Когда оно с увеличением степени полинома перестанет уменьшаться (или это уменьшение незначительно), то нужная степень достигнута.

Я не буду здесь вдаваться в подробности реализации метода наименьших квадратов — это бессмысленно, т. к. его обычно реализуют в виде готовой программы. Такую программу под названием RegrStat вы можете скачать с моей домашней странички по адресу http://revich.lib.ruиз раздела Программы. Умеет строить простейшие регрессионные зависимости и Microsoft Excel, причем в том числе и как функцию от многих переменных, но только первого порядка (линейные полиномы). Ну, и конечно, существует множество специальных программных пакетов для этой цели.

Мы в предыдущем изложении часто упоминали понятие погрешности, приводя его то в процентах, то в абсолютных величинах. Систематизируем эти представления и определим следующие три вида погрешностей:

□ абсолютная погрешность — в единицах измеряемой величины;

□ относительная погрешность — абсолютная, но выраженная в процентах от значения измеряемой величины;

□ относительная приведенная погрешность — абсолютная, но выраженная в процентах либо долях от всего диапазона измерений.

Последняя величина, если она соответствует стандартному ряду (например, 1,0; 0,75; 0,5; 0,25; 0,1 и т. п.), еще называется классом точности и обычно указывается в технических описаниях приборов.

При определении относительной приведенной погрешности учитывают все ошибки (их абсолютные значения): и случайную, и аддитивную, и мультипликативную погрешности. Причем в последнем случае за величину погрешности принимают значение мультипликативной погрешности в конце шкалы — ведь она зависит от измеряемой величины. Отсюда видно, что если мультипликативная погрешность доминирует, то выгоднее как можно больше «ужимать» диапазон измеряемых значений. С другой стороны, аддитивная и случайная погрешности от диапазона не зависят, и уменьшение его приведет к тому, что их вклад увеличится, — в частности, именно поэтому мы старались в схеме на рис. 13.4 «раздуть» выходное напряжение ОУ до максимума, ограничивая максимальный ток значением резистора R7, а не величиной напряжения.