Юрий Ревич - Занимательная электроника

Однако все же интуитивно понятно, что, пока автобус ходит, какое-то, пусть теоретическое, распределение имеется. Такой идеальный бесконечный набор реализаций данного события носит название генеральной совокупности . Именно генеральная совокупность при некоторых условиях может иметь, в частности, нормальное распределение. В реальности же мы имеем дело с выборкой из этой генеральной совокупности. Причем одна из важнейших задач, решаемых в математической статистике, состоит в том, чтобы, имея на руках две разные выборки , доказать, что они принадлежат одной и той же генеральной совокупности — проще говоря, что перед нами есть реализации одного и того же события. Другая важнейшая для практики задача состоит в том, чтобы по выборке определить вид кривой распределения и ее параметры.

На свете сколько угодно случайных событий и процессов, имеющих распределение, совершенно отличное от нормального, однако считается (и доказывается с помощью так называемой центральной предельной теоремы), что в интересующей нас области ошибок измерений, при большом числе измерений и истинно случайном их характере, все распределения ошибок — нормальные. Предположение о большом числе измерений не слишком жесткое — реально достаточно полутора-двух десятков измерений, чтобы все теоретические соотношения с большой степенью точности соблюдались на практике. А вот про истинную случайность ошибки каждого из измерений можно говорить с изрядной долей условности — неслучайными их может сделать одно только желание экспериментатора побыстрее закончить рабочий день. Но математика тут уже бессильна.

Полученные опытным путем характеристики распределения называются оценками параметров, и, естественно, они будут соответствовать «настоящим» значениям с некоторой долей вероятности — наша задача и состоит в том, чтобы определить интервал, в котором могут находиться отклонения оценок от «истинного» значения, и соответствующую ему вероятность. Но настало время все же пояснить — что же это за параметры?

В формуле на рис. 13.6 таких параметра два: величины μ и σ . Они называются моментами нормального распределения (аналогично моментам распределения масс в механике). Параметр μ называется математическим ожиданием (или моментом распределения первого порядка), а величина σ — средним квадратическим отклонением . Нередко употребляют его квадрат, обозначаемый как D или просто σ 2, и носящий название дисперсии (или центрального момента второго порядка).

Математическое ожидание есть абсцисса максимума кривой нормального распределения (в нашем примере с автобусом — это время 10:15), а дисперсия, как видно из рис. 13.6, характеризует «размытие» кривой относительно этого максимума — чем больше дисперсия, тем положе кривая. Эти моменты имеют прозрачный физический смысл (вспомните аналогию с физическим распределением плотностей): математическое ожидание есть аналогия центра масс некоего тела, а дисперсия характеризует распределение масс относительно этого центра (хотя распределение плотности материи в физическом теле далеко от нормального распределения плотности вероятности).

Оценкой m х математического ожидания μ служит хорошо знакомое нам со школы среднее арифметическое:

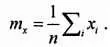
(2)

Здесь n — число измерений; i — текущий номер измерения ( i = 1…., n ); x i — значение измеряемой величины в i -м случае.

Оценка s 2 дисперсии σ 2вычисляется по формуле:

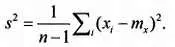
(3)

Оценка среднего квадратического отклонения, соответственно, будет:

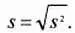
(4)

Здесь ( x i— m х ) — отклонения конкретных измерений от ранее вычисленного среднего.

Следует особо обратить внимание, что сумму квадратов отклонений делить нужно именно на n — 1, а не на n , как может показаться на первый взгляд, иначе оценка получится неверной. Второе, на что следует обратить внимание, — разброс относительно среднего характеризует именно среднее квадратическое отклонение, вычисленное по формулам (3) и (4), а не среднее арифметическое отклонение, как рекомендуют в некоторых школьных справочниках, — последнее дает заниженную и смещенную оценку (не напоминает ли вам это аналогию со средним арифметическим и действующим значениями переменного напряжения из главы 4 ?).

* * *

Заметки на полях

Кроме математического ожидания, средние значения распределения вероятностей характеризуют еще величинами, называемыми модой и медианой. В случае нормального распределения все три величины совпадают, но в других случаях они могут оказаться полезными: мода есть абсцисса наивероятнейшего значения (т. е. максимума на кривой распределения, что полностью отвечает бытовому понятию о моде), а медиана выборки есть такая точка, что половина выборки лежит левее ее, а вторая половина — правее.

* * *

Этими формулами для расчета случайных погрешностей можно было бы ограничиться, если бы не один важный вопрос: оценки-то мы получили, а вот в какой степени они отвечают действительности? Правильно сформулированный вопрос будет звучать так: какова вероятность того, что среднее арифметическое отклоняется от «истинного» значения (т. е. математического ожидания) не более чем на некоторою величину δ (например, на величину оценки среднего квадратического отклонения s )?

Величина δ носит название доверительного интервала , а соответствующая вероятность — доверительной вероятности (или надежности ). Обычно решают задачу, противоположную сформулированной, — задаются величиной надежности и вычисляют доверительный интервал δ . В технике принято задаваться величиной надежности 95 %, в очень уж серьезных случаях — 99 %. Простейшее правило для обычных измерений в этом случае таково: при условии достаточно большого числа измерений (практически, более 15–20) доверительной вероятности в 95 % соответствует доверительный интервал в 2s, а доверительной вероятности в 99 % — доверительный интервал в 3s . Это известное правило трех сигм, согласно которому за пределы утроенного квадратического отклонения не выйдет ни один результат измерения, но на практике это слишком жесткое требование. Если мы не поленимся провести не менее полутора десятков отдельных измерений величины х, то с чистой совестью можем записать, что результат будет равен:

х= m± 2 s.