Пауль Хоровиц - Искусство схемотехники. Том 2 [Изд.4-е]

Рис. 8.13.

Второй вентиль используется в качестве инвентора, в результате этого получается функция И. Лучше понять эту идею вам помогут следующие упражнения.

Упражнение 8.8.Покажите, как сделать с помощью 2-входовых вентилей: а) НЕ из вентилей ИЛИ-НЕ, б) ИЛИ из вентилей ИЛИ-НЕ и в) ИЛИ из вентилей И-НЕ.

Упражнение 8.9.Покажите, как сделать: а) 3-входовую схему И с помощью схемы И на два входа, б) 3-входовую схему ИЛИ с помощью схемы ИЛИ на два входа, в) 3-входовую схему ИЛИ-НЕ с помощью схем ИЛИ-НЕ на два входа, г) 3-входовую схему И с помощью схемы И-НЕ на 2 входа.

Путем многократного использования инвентируемого вентиля (например, И-НЕ) одного типа можно реализовать любую комбинационную функцию. Однако это не относится к неинвентирующему вентилю, так как с его помощью функцию НЕ никаким способом получить нельзя. Именно по этой причине скорее всего вентили И-НЕ получили наибольшее распространение в логических схемах.

Вентиль И будет иметь ВЫСОКИЙ уровень на выходе, когда ВЫСОКИЙ уровень будет действовать на обоих его входах. Если ВЫСОКИЙ уровень обозначает «истину», то «истина» будет на выходе в том случае, если она присутствует на всех входах. Другими словами, при использовании положительной логики вентиль И выполняет логическую функцию И. То же самое касается и вентиля ИЛИ. Что произойдет, если «истину» будет обозначать НИЗКИЙ уровень, как это было в предыдущем примере? Вентиль И даст на выходе НИЗКИЙ уровень, если на любом из его входов была «истина» (НИЗКИЙ уровень), но это функция ИЛИ. С другой стороны, вентиль ИЛИ сформирует НИЗКИЙ уровень лишь в том случае, если «истина» будет на обоих его входах. Но это функция И! Какая путаница!

Существует два пути для разрешения этой проблемы. Первый заключается в том, что уяснив себе суть данной задачи цифрового проектирования, разработчик выбирает такой тип вентиля, который позволит получить требуемый выход, что и было сделано нами ранее. Например, если вам нужно определить, имеет ли один из трех входов НИЗКИЙ уровень, используйте 3-входовой вентиль И-НЕ. По всей вероятности, этим методом пользуется большинство разработчиков цифровых схем. Следуя этим путем, вы начертите вентиль И-НЕ, даже если по отношению к своим входам он выполняет функцию ИЛИ-НЕ (при отрицательной логике). Вероятно, вы при этом обозначите входы, как показано на рис. 8.14.

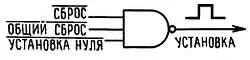
Рис. 8.14.

В данном примере сигналы сброса — СБРОС' (CLEAR)', ОС' — ОБЩИЙ СБРОС, MR' (master reset) и УСТАНОВКА В «0» (RESET), поступающие из различных точек схемы, будут иметь уровни отрицательной логики. Выходной сигнал СБРОС, представленный в положительной логике, будет подаваться на различные устройства, которые должны сбрасываться, если любой из сигналов установки в исходное состояние имеет НИЗКИЙ уровень («истина»).

Другой способ решения задачи сигналов отрицательной логики состоит в использовании метода «заданных уровней». Если вентиль И выполняет функцию ИЛИ, используя на входах отрицательную логику, то изобразите его, как показано на рис. 8.15.

Рис. 8.15.

Вентиль ИЛИ на 3 входа с отрицательными входными сигналами аналогичен по выполняемой функции 3-входовому вентилю И-НЕ. Эта эквивалентность представляет собой важный принцип — свойство логических цепей, который называется теоремой Моргана. Ниже мы кратко рассмотрим некоторые полезные соотношения, идентичные цепи, а сейчас вам достаточно знать, что вы можете заменять И на ИЛИ и наоборот, проинвертировав при этом выход и все входы. На первый взгляд логика заданных уровней может показаться малопривлекательной, поскольку при ее использовании начертание вентилей приобретает странный вид. Но она лучше, чем рассмотренный выше способ, так как логические функции в такой схеме ясно обозначены, применяя эту схему в течение некоторого времени, вы найдете, что она весьма удобна, и не захотите использовать ничего другого. Попробуйте снова решить пример с автомобильной дверцей с помощью логики заданных уровней (рис. 8.16).

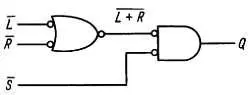
Рис. 8.16.

Левый вентиль определяет, когда L или R имеют «истинное» значение (т. е. НИЗКИЙ уровень), и вырабатывает выходной сигнал в отрицательной логике. Второй вентиль дает на выходе ВЫСОКИЙ уровень, если оба входных сигнала ( L + R ) имеют «истинное» значение, т. е. НИЗКИЙ уровень. Согласно теореме Моргана (через некоторое время она вам уже не потребуется, так как вы будете опознавать эти вентили как равноценные), первый вентиль представляет собой И, а второй вентиль ИЛИ точно так же, как и в ранее изображенной схеме. Следует отметить здесь два важных момента:

1. Термин «отрицательная логика» не означает, что логические уровни имеют отрицательную полярность. Он лишь говорит, что «истинное» утверждение определяется тем из двух состояний, которое имеет меньший уровень (НИЗКИЙ).

2. При символическом изображении вентиля предполагается, что он использует положительную логику. Выполняющий функцию ИЛИ для сигналов отрицательной логики вентиль И-НЕ, может изображаться либо как И-НЕ, либо с использованием логики заданных уровней с обозначением в форме ИЛИ с символами инверсии на входах (маленькие кружки). В последнем случае эти кружки обозначают инверсию входных сигналов, которые поступают на вентиль ИЛИ, работающий при положительной логике, согласно первоначальному определению.

Примечание. Логические функции И и ИЛИ не следует путать с указанными в законах эквивалентными понятиями. В увесистом томе правил, известном под названием «Слова и фразы», свыше 40 страниц посвящается ситуациям, в которых И можно использовать как ИЛИ.

Например, «ИЛИ в случае необходимости можно трактовать как И, а И как ИЛИ». Однако это не имеет ничего общего с теоремой Моргана!

ТТЛ (транзисторно-транзисторная логика) и КМОП (комплементарные МОП-структуры) представляют собой в настоящее время два наиболее распространенных семейства логических элементов. Огромное количество ИМС обоих семейств, выполняющих самые разнообразные функции, выпускаются по меньшей мере десятью фирмами. С помощью этих семейств можно удовлетворить все потребности, которые возникают при построении цифровых схем и устройств. Исключение может составить область схем большой степени интеграции (БИС), в которой преобладают МОП-структуры и сверхбыстродействующая логика, в которой господствуют приборы из арсенида галлия и эмиттерно-связанная логика (ЭСЛ). В дальнейшем в основном будут рассматриваться эти семейства.