Пауль Хоровиц - Искусство схемотехники. Том 1 [Изд.4-е]

Конвертеры отрицательного полного сопротивления и гираторы.Есть два интересных схемных элемента, которые следует упомянуть в любом обзоре: это — конвертер отрицательного полного сопротивления (КОС) и гиратор. Эти устройства могут имитировать свойства катушек индуктивности, хотя в них кроме ОУ используются только конденсаторы и резисторы.

Раз это так, то мы можем делать безиндуктивные фильтры с идеальными свойствами RLС-фильтра, таким образом — это по крайней мере один из способов реализации активных фильтров. КОС преобразует полное сопротивление в ему противоположное (т. е. с обратным знаком), в то время как гиратор преобразует полное сопротивление в обратное (т. е. емкость в индуктивность). Следующие упражнения помогут уяснить, как это происходит.

Упражнение 5.1. Покажите, что изображенная на рис. 5.4 схема представляет собой конвертер полного сопротивления, в частности что Zвх = — Ζ. Подсказка: подайте на вход какое-нибудь напряжение U и вычислите входной ток I . Затем возьмите их отношение, чтобы найти Zвх = U/ I.

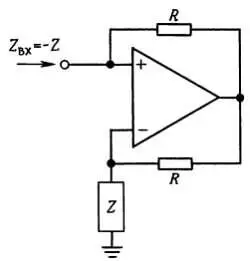
Рис. 5.4. Преобразователь (конвертер) полного отрицательного сопротивления

Упражнение 5.2.Покажите, что схема на рис. 5.5 есть гиратор, в частности что Zвх = R 2/ Z. Подсказка: эту схему можно рассматривать как набор делителей напряжения, начиная справа. Таким образом, КОС превращает конденсатор в «обратную» катушку индуктивности:

ZС= 1/jω C—> Zвх= j/ω C,

т. е. в том смысле, что порождаемый ток запаздывает относительно приложенного напряжения, а его полное сопротивление имеет неправильную частотную зависимость (при возрастании частоты оно не растет, а убывает). Гиратор же, напротив, превращает конденсатор в элемент с истинной индуктивностью:

ZС= 1/jω C—> Zвх= jω CR 2,

т. е. индуктивность которого L= CR 2.

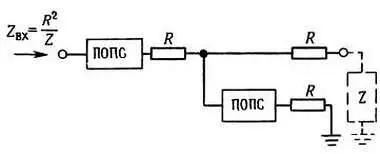
Рис. 5.5.

Существование гиратора делает интуитивно ясным тот факт, что можно построить безындуктивный фильтр, имитирующий любой фильтр, использующий катушки индуктивности: просто заменить каждую катушку «гиратированным» конденсатором. Такое применение гираторов вполне корректно, и ранее упомянутый телефонный фильтр построен именно таким способом. Кроме того, простая вставка гираторов в существующие RLC-схемы позволяет создавать много иных структур фильтров. Проектирование активных безындуктивных фильтров — весьма активно развивающаяся область, и описания новых конструкций появляются в журналах каждый месяц.

Фильтры Саллена и Ки . На рис. 5.6 приведен пример простого фильтра, построенного даже отчасти из интуитивных соображений. Он известен как фильтр Саллена и Ки, по имени его изобретателей. Здесь в качестве усилителя с единичным коэффициентом усиления может использоваться ОУ, включенный в режиме повторителя, либо просто эмиттерный повторитель.

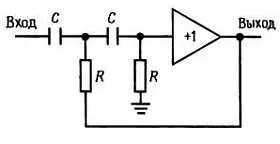
Рис. 5.6.

Данный фильтр представляет собой двухполюсный фильтр верхних частот. Следует отметить, что это был бы просто двухкаскадный RС-фильтр, если бы первый резистор не был соединен с выходом. Легко показать, что на очень низких частотах наклон характеристики такой же, как и у RС-фильтра, поскольку выходной сигнал практически равен нулю. Рост же выходного сигнала при увеличении его частоты приводит к уменьшению ослабления в результате действия этой следящей связи, и за счет этого становится более резким излом характеристики.

Конечно, такое объяснение на пальцах не может заменить полного расчета, уже, к счастью, проделанного для огромного числа хороших фильтров. Мы вернемся к схемам активных фильтров в разд. 5.06 .

При анализе фильтров и при расчете их параметров всегда используются некоторые стандартные термины и имеет смысл придерживаться их с самого начала. Частотная область. Наиболее очевидной характеристикой фильтра является зависимость его коэффициента передачи от частоты; типичный случай — характеристика фильтра нижних частот, показанная на рис. 5.7.

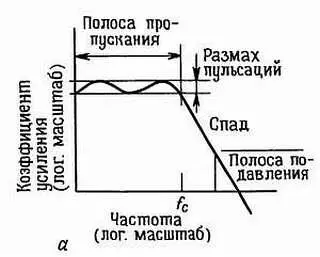
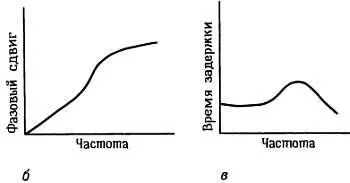
Рис. 5.7. Частотные характеристики фильтров, а— коэффициент усиления (логарифмический масштаб), би в— сдвиг фазы и временное запаздывание (линейный масштаб).

Здесь полоса пропускания представляет собой область частот, которые сравнительно мало ослабляются фильтром. Чаще всего считается, что полоса пропускания простирается до точки, соответствующей значению затухания — 3 дБ, но для некоторых фильтров (среди них замечательны фильтры с «равновеликими пульсациями») граница полосы пропускания может быть определена несколько иначе. Внутри же полосы пропускания характеристика может быть неравномерной, или пульсирующей , с определенным диапазоном (полосой) пульсаций характеристики, как это и показано на рисунке. Частота среза f с определяет границу полосы пропускания. Далее характеристика фильтра проходит через переходную область (известную также как «склон» характеристики фильтра) к полосе задерживания — области значительного ослабления. Полосу задерживания можно определить через некоторое минимальное затухание, например 40 дБ.

Наряду с характеристикой коэффициента передачи в частотной области важен и другой параметр, а именно сдвиг фазы выходного сигнала по отношению к входному. Другими словами, нас интересует комплексная частотная характеристика фильтра, которая обычно обозначается как H( s ), где s= jω; s и Η — комплексные величины. Фазочастотная характеристика важна, поскольку сигнал, целиком расположенный по частоте в полосе пропускания, будет искажен, если время запаздывания при прохождении через фильтр не будет постоянным для различных частот.

Постоянство временной задержки (для всех частот) соответствует линейному возрастанию фазового сдвига в зависимости от частоты, поэтому термин фильтр с линейной фазочастотной характеристикой применяется к идеальному в этом отношении фильтру. На рис. 5.8 показаны типовые графики фазочастотной характеристики и амплитудно-частотной характеристики фильтра нижних частот, который явно не является линейно-фазовым фильтром. Графики фазочастотной характеристики лучше всего строить в линейном по частоте масштабе.