Станислав Горобченко - Курс «Применение трубопроводной арматуры». Модуль «Арматура антипомпажной защиты и регулирования»

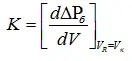(1.14)

где 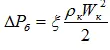– потери давления в сети,

где

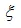– коэффициент сопротивления сети;

ρ k– плотность среды за компрессором;

W k– скорость среды за компрессором.

Геометрический смысл условия (1.13) заключается в том, что угол наклона касательной к характеристике сети должен быть больше угла наклона касательной к характеристике компрессора (это условие выведено для низконапорных турбокомпрессоров, т.е. для вентиляторов и нагнетателей).

Практически это условие в основном не выполняется, т.е. имеется статическая неустойчивость, при расположении рабочих точек на восходящих участках характеристик компрессоров, при этом допустимо использование упрощенного условия статической устойчивости по (1.12).

Динамическая устойчивость турбокомпрессоров в отличии от статической связана не с величиной расхода среды и формой характеристик в зоне рабочей точки, а со скоростью изменения расхода среды.

Применительно к турбонагнетателям выведен критерий динамической неустойчивости в виде условия

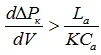, (1.15)

где L a– акустическая масса трубопровода (сети),

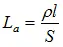, (1.16)

где

ρ – плотность среды;

l – длина трубопровода;

S – площадь сечения трубопровода;

C a– акустическая гибкость,

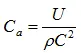(1.17)

где

U – объем трубопровода;

C – скорость звука в среде.

При этом условии самовозбуждение колебаний возможно и на нисходящих участках характеристики компрессора. Возбуждение возможно при сколько угодно малом возмущении (отклонении от равновесного режима), т.е. мягкое возбуждение с последующим нарастанием амплитуды колебаний.

Существует также возможность динамической неустойчивости при воздействии сильного возмущения на систему (жесткое возбуждение колебаний).

На практике помпаж, вызванный потерей динамической устойчивости, встречается довольно редко, а реализовать его подавление путем смещения рабочей точки сложно (устойчивость обеспечивается правильной увязкой компрессора и сети еще на стадии проектирования системы).

В основном системы антипомпажного регулирования направлены на подавление помпажа, вызванного статической неустойчивостью. При других видах помпажа, в том числе от динамической неустойчивости, которые могут происходить при работе на нисходящих участках характеристик (система статически устойчива), используют не антипомпажное регулирование, а защиту путем аварийного останова компрессора или байпасированием всего расхода.

Образование установившихся помпажных колебаний может быть пояснено с использованием характеристики компрессора для прямого и обратного хода при

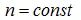
Исходя из принятого условия статической устойчивости ,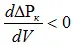

на сетке размерных характеристик

или

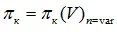
возможно нанести теоретическую линию (границу) помпажа, проходящую через экстремумы характеристик (эта граница условная, т.к. не учитывается динамическая неустойчивость и влияние сети в системе компрессор-сеть).

Выходные характеристики зависят от частоты вращения ротора следующим образом:

– производительность пропорциональна частоте вращения;

– напор пропорционален квадрату частоты вращения;

– требуемая мощность пропорциональна кубу скорости вращения.

Этот закон вытекает из теории подобия при и .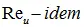

На характеристике политропного напора граница помпажа соответствует точке, где степень сжатия максимальна. Эта точка располагает между точками, соответствующими максимальному политропному напору и максимальному политропному КПД.

Применение законов подобия показывает, что величина политропного напора на границе помпажа изменяется пропорционально квадрату соответствующего объемного расхода на всасывании. Поэтому принимают форму линии помпажа в виде квадратичной параболы (при этом следует проверять применимы ли законы подобия во всем диапазоне режимов по частоте вращения.

Помпаж является нестационарным процессом, вызванным глобальной потерей устойчивости. При этом помпажу предшествует вращающийся срыв, т.е. помпаж физически является следствием срывных течений, изучаемых аэродинамикой.

Вращающийся срыв на передних кромках лопаток порождается срывом потока с лопаток при углах атаки i 1 больше критических. Для центробежного компрессора срывные углы атаки соответствуют

.

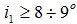При постоянной частоте вращения и уменьшении объемного расхода и, соответственно, абсолютной скорости C 1на входе в компрессор возрастает угол вектора относительной скорости W 1, т.е. угол атаки на входе в лопатки i 1, что вытекает из анализа треугольника скоростей. Исходя из этого можно полагать, что граница помпажа соответствует углам атаки 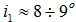, что в принципе обуславливает возможность теоретического определения границы помпажа по треугольникам скоростей на входе в компрессор.

Однако, на фактическую границу помпажа влияет система "компрессор-сеть" в целом. Поэтому в каждом конкретном случае требуется проведение испытаний для уточнения границы помпажа.