М. Бабаев - Гидравлика

Гидростатика изучает жидкость в ее равновесном состоянии.

Кинематика жидкости изучает жидкость в движении, не рассматривая сил, порождавших или сопровождавших это движение.

Гидродинамика также изучает движение жидкости, но в зависимости от воздействия приложенных к жидкости сил.

В кинематике используется сплошная модель жидкости: некоторый ее континуум. Согласно гипотезе сплошности, рассматриваемый континуум – это жидкая частица, в которой беспрерывно движется огромное количество молекул; в ней нет ни разрывов, ни пустот.

Если в предыдущих вопросах, изучая гидростатику, за модель для изучения жидкости в равновесии взяли сплошную среду, то здесь на примере той же модели будут изучать жидкость в движении, изучая движение ее частиц.

Для описания движения частицы, а через нее и жидкости, существуют два способа.

1. Метод Лагранжа. Этот метод не используется при описании волновых функций. Суть метода в следующем: требуется описать движение каждой частицы.

Начальному моменту времени t 0соответствуют начальные координаты x 0, y 0, z 0.

Однако к моменту t они уже другие. Как видно, речь идет о движении каждой частицы. Это движение можно считать определенным, если возможно указать для каждой частицы координаты x, y, z в произвольной момент времени t как непрерывные функции от x 0, y 0, z 0.

x = x(x 0, y 0, z 0, t)

y =y (x 0, y 0, z 0, t)

z = z(x 0, y 0, z 0, t) (1)

Переменные x 0, y 0, z 0, t, называют переменными Лагранжа.

2. Метод определения движения частиц по Эйлеру. Движение жидкости в этом случае происходит в некоторой неподвижной области потока жидкости, в котором находятся частицы. В частицах произвольно выбираются точки. Момент времени t как параметр является заданным в каждом времени рассматриваемой области, которая имеет координаты x, y, z.

Рассматриваемая область, как уже известно, находится в пределах потока и неподвижна. Скорость частицы жидкости u в этой области в каждый момент времени t называется мгновенной местной скоростью.

Полем скорости называется совокупность всех мгновенных скоростей. Изменение этого поля описывается следующей системой:

u x= u x(x,y,z,t)

u y= u y(x,y,z,t)

u z= u z(x,y,z,t)

Переменные в (2) x, y, z, t называют переменными Эйлера.

Сутью вышеупомянутого поля скоростей являются векторные линии, которые часто называют линиями тока.

Линия тока – такая кривая линия, для любой точки которой в выбранный момент времени вектор местной скорости направлен по касательной (о нормальной составляющей скорости речь не идет, поскольку она равна нулю).

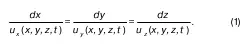
Формула (1) является дифференциальным уравнением линии тока в момент времени t. Следовательно, задав различные ti по полученным i, где i = 1,2, 3, …, можно построить линию тока: ею будет огибающая ломаной линии, состоящей из i.

Линии тока, как правило, не пересекаются в силу условия ≠ 0 или ≠ ∞. Но все же, если эти условия нарушаются, то линии тока пересекаются: точку пересечения называют особой (или критической).

1. Неустановившееся движение, которое так называется иззза того, что местные скорости в рассматриваемых точках выбранной области по времени изменяются. Такое движение полностью описывается системой уравнений.

2. Установившееся движение: поскольку при таком движении местные скорости не зависят от времени и постоянны:

u x= u x(x,y,z)

u y= u y(x,y,z)

u z= u z(x,y,z)

Линии тока и траектории частиц совпадают, а дифференциальное уравнение для линии тока имеет вид:

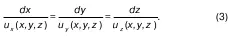
Совокупность всех линий тока, которые проходят через каждую точку контура потока, образует поверхность, которую называют трубкой тока. Внутри этой трубки движется заключенная в ней жидкость, которую называют струйкой.

Струйка считается элементарной, если рассматриваемый контур бесконечно мал, и конечной, если контур имеет конечную площадку.

Сечение струйки, которое нормально в каждой своей точке к линиям тока, называется живым сечением струйки. В зависимости от конечности или бесконечной малости, площадь струйки принято обозначать, соответственно, ω и dω.

Некоторый объем жидкости, который проходит через живое сечение в единицу времени, называют расходом струйки Q.

Особенности видов движения, рассматриваемых в гидродинамике.

Можно выделить следующие виды движения.

Неустановившееся, по поведению скорости, давления, температуры и т. д.; установившееся, по тем же параметрам; неравномерное, в зависимости от поведения тех же параметров в живом сечении с площадью; равномерное, по тем же признакам; напорное, когда движение происходит под давлением p > p атм, (например, в трубопроводах); безнапорное, когда движение жидкости происходит только под действием силы тяжести.

Однако основными видами движения, несмотря на большое количество их разновидностей, являются вихревое и ламинарное движения.

Движение, при котором частицы жидкости вращаются вокруг мгновенных осей, проходящих через их полюсы, называют вихревым движением.

Это движение жидкой частицы характеризуется угловой скоростью, компонентами (составляющими), которой являются:

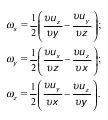
Вектор самой угловой скорости всегда перпендикулярен плоскости, в которой происходит вращение.

Если определить модуль угловой скорости, то

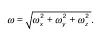
Удвоив проекции на соответствующие координаты оси ω x, ω y, ω z, получим компоненты вектора вихря

θ = 2ω.

Совокупность векторов вихря называется векторным полем.

По аналогии с полем скоростей и линией тока, существует и вихревая линия, которая характеризует векторное поле.

Это такая линия, у которой для каждой точки вектор угловой скорости сонаправлен с касательной к этой линии.

Линия описывается следующим дифференциальным уравнением:

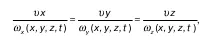
в котором время t рассматривается как параметр.

Вихревые линии во многом ведут себя так же, как и линии тока.

Вихревое движение называют также турбулентным.

Это движение, называют также потенциальным (безвихревым) движением.

При таком движении отсутствует вращение частиц вокруг мгновенных осей, которые проходят через полюсы жидких частиц. По этой причине: