Вадим Грибунин - Цифровая стеганография

Для извлечения ЦВЗ используется инверсная формула, аналогичная (6.4).

Данный алгоритм позволяет скрыть довольно большой объем данных в исходном изображении: до четверти от размеров исходного изображения.

А30 (D.Kundur [14]).

Также, как и в предыдущем алгоритме, исходное и внедряемое изображения подвергаются вейвлет-преобразованию. Для встраивания используются все коэффициенты детальных поддиапазонов.

Множество этих коэффициентов разбивается на неперекрывающиеся блоки размером 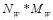. Блоки обозначаются 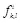, где 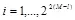, а k и l , соответственно местоположение коэффициента и уровень разрешения.

Водяной знак прибавляется к элементам исходного изображения по формуле

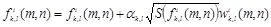, (6.28)

где S — коэффициент масштаба, вычисляемый по формуле

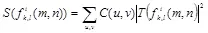, (6.29)

C ( u,v ) — взвешивающая матрица, определяющая частотную чувствительность системы зрения человека, Т — оператор ДПФ.

Таким образом, алгоритм использует довольно сложную модель человеческого зрения. Для обнаружения в детекторе может быть использовано как вычисление корреляционной функции, так и визуальное сравнение.

Под квантованием понимается процесс сопоставления большого (возможно и бесконечного) множества значений с некоторым конечным множеством чисел. Понятно, что при этом происходит уменьшение объема информации за счет ее искажения. Квантование находит применение в алгоритмах сжатия с потерями. Различают скалярное и векторное квантование. При векторном квантовании, в отличии от скалярного, происходит отображение не отдельно взятого отсчета, а их совокупности (вектора). Из теории информации известно, что векторное квантование эффективнее скалярного по степени сжатия, обладая большей сложностью. В стеганографии находят применение оба вида квантования.

В кодере квантователя вся область значений исходного множества делится на интервалы, и в каждом интервале выбирается число его представляющее. Это число есть кодовое слово квантователя и обычно бывает центроидом интервала квантования. Множество кодовых слов называется книгой квантователя. Все значения, попавшие в данный интервал, заменяются в кодере на соответствующее кодовое слово. В декодере принятому числу сопоставляется некоторое значение. Интервал квантования обычно называют шагом квантователя.

Встраивание информации с применением квантования относится к нелинейным методам. В работе [41] было показано, как может быть построена подобная «слепая» стегосистема, пропускная способность которой эквивалентна пропускной способности стегосистемы, имеющей на приеме исходный сигнал. При этом делается предположение о гауссовском характере исходного сигнала.

Модель стегосистемы, не требующей наличия исходного сигнала в декодере представлена на рис. 6.3.

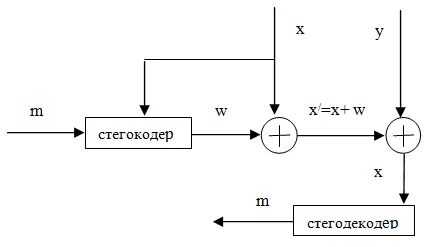
Рис. 6.3 Модель «слепой» стегосистемы

Передаваемое сообщение m имеет ограниченную энергию для выполнения требования его незаметности. Помехами являются исходный сигнал и еще одна гауссовская помеха — шум обработки (квантования). Кодеру исходный сигнал известен, декодер должен извлечь ЦВЗ m без знания обеих составляющих помех. В работе [40] Костасом предложен метод борьбы с помехами, который, однако, является непрактичным в силу необходимости выполнения полного перебора кодовых слов в книге большого размера. Поэтому, были предложены многочисленные улучшения метода Костаса, заключающиеся в применении различных структурированных квантователей (например, решетчатых или древовидных).

Как было показано в главе 5, наиболее предпочтительно внедрение информации в спектральную область изображения. Если при этом используются линейные методы, то встраивание ЦВЗ производят в средние полосы частот. Это объясняется тем, что энергия изображения сосредоточена, в основном, в низкочастотной (НЧ) области. Следовательно, в детекторе ЦВЗ в этой области наблюдается сильный шум самого сигнала. В высокочастотных (ВЧ) областях большую величину имеет шум обработки, например, сжатия. В отличие от линейных, нелинейные схемы встраивания информации могут использовать НЧ области, так как мощность внедряемого ЦВЗ не зависит от амплитуды коэффициентов. Это объясняется тем, что в нелинейных алгоритмах скрытия не используется корреляционный детектор, коэффициенты малой и большой амплитуды обрабатываются одинаково.

Итак, как показано на рис. 6.3, внедряемый ЦВЗ m определенным образом модулируется и складывается с исходным сигналом x , в результате чего получается заполненный контейнер s(x,m) . Этот контейнер может рассматриваться и как ансамбль функций от x , проиндексированных по m , т. е. s m(x) . Эти функции обладают следующими свойствами:

— каждая из них должна быть близка, визуально неотличима от x ;

— точки одной функции должны находиться на достаточном расстоянии от точек другой функции, чтобы обеспечить возможность робастного детектирования ЦВЗ.

В качестве таких функций может выступать семейство квантователей. Число всевозможных m определяет необходимое число квантователей; индекс m определяет используемый квантователь для представления ЦВЗ m . Для случая m = 2 мы получаем бинарный квантователь. На рис. 6.4 поясняется принцип встраивания информации с применением модуляции индекса квантования (МИК). Для вложения бита , точка изображения отображается в одно из близлежащих кодовых слов. Минимальное расстояние между кодовыми словами различных квантователей определяет робастность схемы ЦВЗ.

В работе [38, 39] рассматривается применение в схеме МИК так называемого дизеризованного квантователя. Дизеризация заключается в том, что перед квантованием к сигналу добавляется некоторое число d i , которое вычитается после квантования:

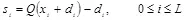. (6.30)