Хаим Шапира - Гладиаторы, пираты и игры на доверии. Как нами правят теория игр, стратегия и вероятности

В другой версии ультимативной игры несколько человек предлагают разделить общую сумму по-разному. Тот, кто «отвечает», может выбрать одно предложение, а остаток уходит тому, кто «предлагал». Здесь реальность и математика едины. В математическом решении некто предлагает всю сумму целиком – это будет равновесие Нэша (позже мы о нем поговорим, но вкратце это означает, что если сумма в игре составляет $100 и кто-либо из игроков предлагает ее, то никто не может предложить ничего лучше – все суммы будут меньше, и тот, кто отвечает на предложение, естественно, отвергнет все остальные). На самом деле, когда люди хотят, чтобы их предложение приняли, и боятся, что другие предложат больше, они склонны предлагать почти всю сумму .

Есть еще одна версия ультимативной игры. В ней только два игрока, и тот, кто вносит предложение, «диктатор», обладает полным контролем, а тот, кто принимает или отвергает предложение, должен принять любой предложенный вариант – и, по сути, представляет собой «пустое место». Согласно математическому решению, предлагающий просто берет всю сумму и уходит. Как вы уже, наверное, догадались, стандартные экономические предпосылки – это весьма неточный способ предсказать реальное поведение. Очень часто всю сумму не удерживают: «диктаторы» склонны давать другому игроку какую-то часть денег (иногда они дают довольно большие суммы, а порой даже делят сумму поровну). Зачем? Чему это учит нас о человеческой природе? Какая здесь связь с альтруизмом, добротой, честностью и самоуважением? Об этом я знаю не больше вас.

В следующей главе мы узнаем о нескольких играх – и забавных, и познавательных, расширим наш игровой лексикон, узнаем кое-что новое и поучимся тому, как мыслить стратегически, а помимо этого познакомимся с тем, кого я считаю «Стратегом года». Итак, играем!

«Доверять ненадежным можно всегда. Ты всегда можешь положиться на то, что они ненадежны. А вот надежным… о, им ни в коем случае нельзя доверять».

Банда пиратов после тяжелого рабочего дня возвращается домой и несет 100 золотых дублонов, которые предстоит разделить между пятью лучшими пиратами: это Эйб, Бен, Кэл, Дон и Эрн. Эйб – глава банды, а Эрн – подчиненный самого низкого ранга.

Несмотря на иерархию, группа демократична, и именно потому добычу решают делить по следующему принципу. Эйб предлагает формулу распределения, и все пираты (включая его самого) за нее голосуют. Если большинство ее одобряет, идея воплощается в жизнь – и все, конец игры; а если нет, то Эйба бросают в океан (даже пираты-демократы довольно непокорны). И если Эйба больше с нами нет, настает очередь Бена. Он предлагает, пираты голосуют снова. Обратите внимание: теперь возможно равенство голосов. Предположим, что в таком случае предложение отвергается, а того, кто его выдвинул, бросают в океан (хотя есть и другая версия игры, при которой за предложившим остается право решающего голоса). Итак, если предложение Бена получает одобрение большинства пиратов, его идею воплощают в жизнь; если нет, его бросают в океан, и свое предложение для коллектива (уже не столь большого) будет выдвигать Кэл. И так далее.

Игра продолжается до тех пор, пока какое-либо предложение не примут большинством голосов. Если этого не случится, Эрн остается последним пиратом и забирает все 100 дублонов.

Прежде чем читать дальше, пожалуйста, остановитесь и немного подумайте о том, чем должна закончиться эта игра. И учтите: пираты умны и жадны.

Математическое решение

Математики решают этот вопрос при помощи «обратной индукции» – идут от конца к началу. Предположим, что мы находимся на той стадии игры, когда отвергнуты идеи и Эйба, и Бена, и Кэла – да, Кэл тоже подкачал. Остались только Дон и Эрн, и теперь решение очевидно: Дон должен предложить Эрну забрать все 100 дублонов – или тоже отправиться на свидание к акулам (напомним, равенство голосов означает, что предложение провалено), которое долго не продлится. Дон – умный пират и предлагает Эрну забрать всю добычу.

Кэл тоже умен и знает, что именно таким будет финал игры (если до него дойдет, чего сам Кэл надеется любой ценой избежать). Более того, он знает, что ему нечего предложить Эрну – ведь интерес Эрна именно в том, чтобы любыми средствами до этого финала добраться. Впрочем, Кэл может помочь Дону и улучшить его положение – по сравнению с тем, что случится, если Дон останется один на один с Эрном. И Кэл может сделать так, чтобы Дон проголосовал за него, предложив ему один дублон (в этом случае Дон отдаст свой голос за идею Кэла, сам Кэл проголосует за себя, и вместе они составят большинство). Итак, при трех игроках монеты распределяются так: Кэл – 99, Дон – 1, Эрн – 0.

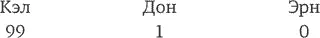
Естественно, Бен понимает все эти калькуляции. Он знает, что не может ничем улучшить положение Кэла, но вот Дону и Эрну он может сделать предложение, от которого те не смогут отказаться. И выглядит все так: Кэлу не достается ничего, Эрн получает 1 монету, Дон – 2, а Бен забирает оставшиеся 97.

И теперь мы переходим к той стадии, когда легко увидеть, как должен действовать Эйб (он – главарь, и он очень опытен в дележе добычи). Эйб предлагает вот что. Он забирает 97 монет, не дает ни гроша Бену (которого не купить ни при каких раскладах), дает 1 монету Кэлу (это лучше, чем 0 монет, а именно столько получит Кэл, если Эйб отправится в плавание и право хода уйдет к Бену); Дон тоже не получает ничего; а Эрну достаются 2 монеты (купить голос Эрна легче, чем голос Дона). Это предложение одобряют трое пиратов, против него выступают двое – и морские разбойники отправляются грабить корабли до тех пор, пока не обмелеют все моря.

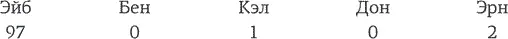
Последнее распределение кажется довольно странным. Придем ли мы к нему, если в таком же положении окажутся пять студентов-математиков? А что насчет эксперимента с пятью аспирантами-психологами? Как все эти возможности разрешат они?

Позволено ли игрокам вступать в союзы и заключать сделки? И если так, на что будет похожа игра? Математическое решение всегда предполагает, что все игроки разумны и рациональны – но разумно ли делать такое допущение? Рационально ли это? (Я не раз наблюдал за этой игрой и никогда не видел, чтобы участники делили деньги в соответствии с математическим решением. К чему бы это?) Математическое решение игнорирует важные эмоции: зависть, обиду, злорадство при виде чужих страданий… Могут ли чувства изменить математический расчет?