Хаим Шапира - Гладиаторы, пираты и игры на доверии. Как нами правят теория игр, стратегия и вероятности

В любом случае, хотя распределение Эйба – 97, 0, 1, 0, 2 – математически справедливо, я бы посоветовал ему проявить великодушие и предложить сотоварищам-пиратам разделить добычу так: 57, 10, 11, 10, 12 (то есть «накинуть» каждому еще по десятке из своей доли в 97 монет). Есть надежда, что так команда будет довольна и мятежа не произойдет.

И если «Пиратская забава» – версия ультимативной игры для многих игроков – кажется вам странной, то что вы скажете о следующей игре?

Умирает старик-богач. У него двое детей – Сэм и Дэйв [8] Эта история основана на знаменитой игре «Сороконожка», которую впервые представил в 1981 г. Роберт Розенталь. . Братья на дух не переносят друг друга. Они уже десять лет не виделись и не общались и только сейчас встречаются в доме отца, чтобы услышать его последнюю волю и прочесть завещание.

Нотариус вскрывает конверт и зачитывает необычный документ. Оказывается, отец оставил сыновьям миллион и десять тысяч долларов – и ряд вариантов того, как те могут делить эти деньги.

Вариант первый: Сэм, старший брат, может взять себе $100, дать младшему брату $1, а остальное раздать на благотворительность (да, это будет очень милосердно!).

Сэм не обязан соглашаться и может передать право дележа младшему брату. Если деньгами распоряжается Дэйв, он забирает $1000, Сэм получает $10, а остальное уходит на благотворительность. Это второй вариант.

Но от такого, при желании, может отказаться и Дэйв – и право владения снова переходит к Сэму, а деньги делят так: Сэм забирает $10 000, отдает Дэйву $100, а остальное… ну, вы поняли.

Впрочем, теперь (да, это вы тоже поняли) Сэм снова не обязан соглашаться. У него есть право отдать «ход» Дэйву, а тому позволено разделить деньги так: забрать себе $100 000, отдать Сэму $1000, а остаток, ставший уже чуть меньше, направить на милосердные дела.

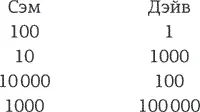
Но и это не вырезано на скрижалях. Дэйв может решить, что позволит Сэму снова делить деньги, но тогда все пройдет так: Сэм заберет $1 млн себе, $10 000 оставит ненавистному брату, а на дела милосердия не пойдет ничего.

И как думаете, что случится? Опять же, разрешить этот вопрос нам поможет обратная индукция. Кто угодно поймет, что игра никогда в жизни не продлится до последнего пятого раунда: Дэйв не позволит Сэму забрать миллион, поскольку это снизит его личную выгоду со $100 000 до $10 000. Сэм это знает и ни за что не позволит игре дойти до четвертого раунда, в котором он получает только $1000 – вместо $10 000, которые достаются ему в третьем раунде. Продолжите сами, и вы увидите: игра не дойдет даже до третьего раунда… да и до второго она тоже не дойдет. Это поражает, но, если предположить, что оба брата принадлежат к одному виду, Homo economicus statisticus (то есть они способны производить расчеты и стремятся к собственной выгоде), игра закончится на первом же раунде: Сэм забирает $100, дает Дэйву $1, а остальная огромная сумма идет на благие дела (плохие намерения могут привести к благому исходу, а братья потом, возможно, обретут награду на небесах). Это математическое решение: $100 для Сэма, $1 для Дэйва и очень много денег на милосердие.

Есть ли в этом логика? Решите сами.

Это довольно простая игра, более известная как «Хрум!» (Chomp!). За ее формулировку с плитками шоколада, которую использую я, мы в долгу перед ныне покойным американским математиком Дэвидом Гейлом. В нее играют на шахматной доске, каждая клеточка которой сделана из шоколада, но при этом крайняя левая клетка содержит смертельный яд. Вот правила.

Игрок, делающий первый ход, ставит отметку X на одной из клеток, выбирая ее по желанию.

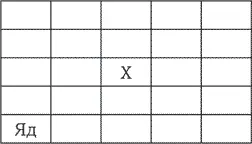
После этого все клетки, расположенные и справа, и сверху от клетки с отметкой X, получают такую же отметку.

Теперь очередь второго игрока. Он отмечает какую-либо из клеток, оставшихся свободными, как О. Как только это произойдет, все пустые клетки справа и сверху от нее тоже получают такую отметку.

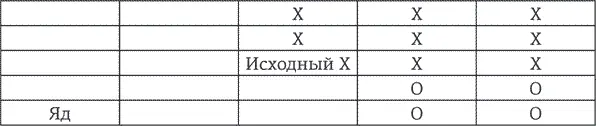
Потом первый игрок снова ставит отметку X, отчего такую же получают помеченная клетка и все клетки справа и сверху от нее (если таковые есть), а второй игрок ставит очередную отметку O – на выбранную клетку и все клетки справа и сверху от нее (если таковые есть). Игра длится до тех пор, пока кому-либо из игроков не придется выбрать яд, тогда он проигрывает и умирает (конечно же метафорически).

С радостью приглашаю вас сыграть в эту игру на доске 7×4 (7 рядов и 4 колонки, или наоборот).

Если играть в эту игру на квадрате (с равным числом рядов и колонок), то есть стратегия, следуя которой игрок, делающий первый ход, всегда побеждает. Сможете ее найти? Возьмите три минуты на размышление.

Решение: Пусть в игру играют Джоан и Джилл. Если Джоан ходит первой, она должна придерживаться следующей стратегии – и непременно одержит победу. На первом ходу она должна выбрать клетку, расположенную справа по диагонали от клетки с пометкой «Яд».

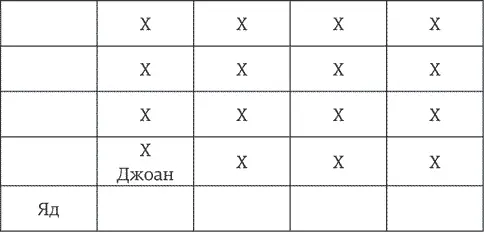
Теперь все, что ей нужно делать, – это симметрично повторять ходы противника; иными словами, делать тот же ход, что и Джилл, только на противоположной стороне доски. Картинка, приведенная ниже, объяснит это лучше всяких слов.

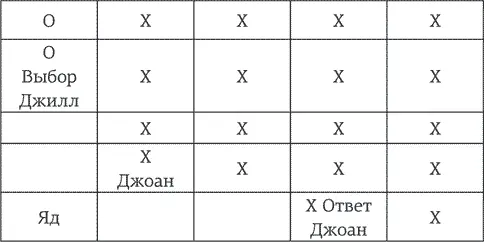
То, как победить в этой игре, теперь должно быть совершенно ясно.

Все становится намного сложнее, если играть на прямоугольнике. Но и тогда можно доказать, что у игрока, делающего первый ход, есть выигрышная стратегия, проблема только в том, что доказательство не определяет ее точно. В математике такой вид доказательств называют «неконструктивным доказательством существования».