Хаим Шапира - Гладиаторы, пираты и игры на доверии. Как нами правят теория игр, стратегия и вероятности

Студенты, изучающие теорию вероятностей, сказали бы: «Вам не найти равномерное распределение для множества рациональных чисел». Впечатляет?

Если вы не понимаете, что это значит, превосходно! Лучшая версия этого парадокса не имеет никакого отношения к вероятностям. Она появляется в книге «Сатана, Кантор и бесконечность», прекрасном произведении (с прекрасным названием, правда?) Рэймонда Смаллиана, американского математика, философа, классика-пианиста и фокусника [11] Smullyan Raymond M . Satan, Cantor, and Infinity: And Other Mind-Boggling Puzzles. Alfred A. Knopf, New York, 1992; Dover Publications, 2009. . Смаллиан представляет две версии парадокса:

1. Если в вашем конверте B банкнот, то вы либо получите B, либо потеряете ½ B, заменив этот конверт другим. Следовательно, вам следует их поменять.

2. Если конверты содержат соответственно С и 2 С , а вы решаете заменить один на другой, то вы либо получите С, либо потеряете С, так что шансы равны и вы можете получить столько же, сколько рискуете потерять.

Вы в растерянности? Я тоже.

В любом случае многие пессимистично заявляют, что здесь нет никакого парадокса, просто такова жизнь, и не имеет значения, что вы сделаете или куда пойдете: лучше всегда будет там, где нас нет. Например, если вы в браке – возможно, вам следовало никогда в него не вступать. В конце концов, как писал Чехов: «Если боитесь одиночества, то не женитесь». И все же, если решите остаться в одиночестве, вы снова неправы. В Библии слова «не хорошо» впервые встречаются в Книге Бытия: «…не хорошо быть человеку одному…» (2: 18). Это не я сказал, а Господь Бог.

«Золотые шары» (Golden Balls) – британское телевизионное шоу, выходившее в эфир с 2007 по 2009 г. Не будем вдаваться в детали правил и ходов, но на последней стадии игры двое оставшихся игроков должны договориться о том, как разделить между собой определенную сумму денег. У каждого игрока – два шара с наклейками: на одном написано SPLIT («Дележ»), на другом – STEAL («Кража»). Если оба решают выбрать «Дележ», деньги делят поровну; если оба выбирают «Кражу», то остаются ни с чем; а если их выбор не совпадает, тогда приз забирает тот, кто выбрал «Кражу». Сперва игроки могут обсудить то, как им поступить, – и только потом делать выбор.

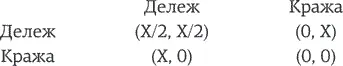
C первого же взгляда на таблицу, основанную на правилах игры, совершенно ясно одно: если каждый думает лишь о своей выгоде, то «Кража» лучше, чем «Дележ». Но есть проблема: если каждый из игроков думает только о себе, проигрывают оба. (Да, это в какой-то мере похоже на «Дилемму заключенного», о которой вы, возможно, уже знаете. Эту знаменитую дилемму мы обсудим позже.)

В большинстве случаев игроки пытаются убедить друг друга выбрать «Дележ», и иногда это срабатывает. На YouTube немало записей игры с душераздирающими сценами, когда игроки, доверявшие противнику, выбирали «Дележ» – лишь для того, чтобы жестоко обмануться.

Однажды игрок по имени Ник применил неожиданный подход. Он сказал своему сопернику Ибрагиму, что выберет «Кражу», и умолял того решиться на «Дележ», обещая разделить деньги (в этом случае приз £13 600) между ними после того, как игра окончится. Ибрагим не мог поверить своим ушам: Ник снова и снова обещал сжульничать! Но почему тогда он говорил об этом заблаговременно? Да потому, говорил Ник, что я принципиально честен! «Будет тебе твоя половина, Ибрагим! Выбери “Дележ”, а то проиграешь! – говорил Ник. – Тебе все только на пользу!» В этот момент игроков попросили прекратить диалог и взять шар.

Ибрагим выбрал «Дележ» – но то же самое сделал и Ник! Почему? Просто он был на все сто уверен, что убедил Ибрагима! Так к чему лишние проблемы? Зачем делить деньги после игры? Делим прямо сейчас!

Остается лишь признать, что Ник, вероятно, был достоин звания «Стратег года».

Эта игра посвящена не только стратегиям переговоров, но и доверию между игроками.

(Все, что написано ниже, предназначено только для любителей шахмат и математики.)

Многие считают, что теория игр появилась в 1944 г., с выходом в свет каноничной книги «Теория игр и экономическое поведение», авторами которой стали великий математик Джон фон Нейман (1903–1957) и экономист Оскар Моргенштерн (1902–1977). (Впрочем, проблемы, к которым обращается теория игр, в той или иной мере существовали с начала времен. Первые примеры можно обнаружить в Талмуде, в трактате Сунь Цзы «Искусство войны» и в произведениях Платона.)

Но все же некоторые склонны полагать, что теория игр – как дисциплина – зародилась в 1913 г., когда немецкий математик Эрнст Цермело (1871–1953) представил свою теорему о шахматах, «игре королей»: «Либо белые могут форсировать выигрыш, либо черные могут форсировать выигрыш, либо обе стороны могут по крайней мере форсировать ничью». Другими словами, он утверждал, что существует всего три варианта:

1. У белых есть стратегия, следование которой всегда ведет к победе.

2. У черных есть стратегия, следование которой всегда ведет к победе.

3. И у белых, и у черных есть сочетание стратегий, следование которым всегда ведет к ничьей.

Помню, когда я впервые прочел эту теорему, то подумал (со своим обычным сарказмом): «Ух ты! Как умно… и как ново… Немецкий знаток говорит мне, что победят либо белые, либо черные, либо все кончится ничьей. А я-то думал, тут столько вариантов…» И только вчитавшись в строки доказательства, я понял, в чем именно состоит теорема.

По сути, Цермело доказал, что игра в шахматы неотличима от имеющей предел (3×3) игры в «крестики-нолики». Мы уже упоминали: если в партии в «крестики-нолики» оба игрока не сошли на время с ума (да, иногда такое бывает), все игры всегда закончатся вничью. Иного варианта нет. Даже те, кто раз за разом проигрывает в «крестики-нолики», в конце концов сумеют понять, как не проигрывать никогда, и это превратит игру, и так не особо захватывающую, в нечто столь же скучное, как чтение книги с белыми страницами без текста.

Цермело сумел доказать, что шахматы (и многие другие игры) представляют собой практически те же «крестики-нолики» и отличие – не в качестве, а в количестве.

В шахматах «стратегия» – это набор ответов на любое положение, какое только может возникнуть на доске. Ясно, что у двух игроков может быть огромное множество стратегий. Отметим стратегии белых (первого игрока) буквой S, а стратегии его противника – буквой Т. Как мы уже сказали, теорема Цермело говорит о существовании лишь трех вариантов:

либо у белых есть стратегия (назовем ее S4), при которой они побеждают всегда, независимо от действий черных…