Хаим Шапира - Гладиаторы, пираты и игры на доверии. Как нами правят теория игр, стратегия и вероятности

Одним из самых ценных навыков, которые я получил в средней школе в родном Вильнюсе, столице Литвы, было умение играть в стратегические игры на листочке бумаги, в классе, тайком от учителей. Мне очень нравилась «бесконечная» версия «крестиков-ноликов»: они часто помогали мне выжить на скучных уроках.

Думаю, большинству знакома классическая версия игры с полем 3×3. Шестилеток она приводит в восторг. Дети постарше и взрослые, как правило, сводят все поединки вничью, если только один из игроков не уснет на середине партии (это имеет смысл, игра все-таки скучная). Впрочем, в «бесконечной» версии игра проходит на поле с бесконечной решеткой, а цель – выстроить последовательность из пяти крестиков или ноликов, которая, как и в обычной игре, может быть горизонтальной, вертикальной и диагональной. Игроки по очереди ставят на клетки поля X или O (по предварительному соглашению), и первый, кому удастся сформировать «пятерку», побеждает.

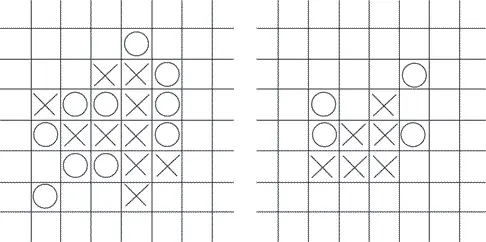
На рисунке слева игрок, выбравший «крестики», уже победил.

На рисунке справа ход игрока, выбравшего «нолики», – но он ничем не может помешать противнику одержать победу. Видите почему?

В те далекие школьные дни я верил в то, что сам изобрел эту игру, но со временем, в должный час, понял, что я далек от правды. Оказалось, сходная игра под названием гомоку была на протяжении многих лет очень популярна в Японии и Вьетнаме. «Го» в переводе с японского означает «пять». Хотя в гомоку иногда играют на той же доске, что и в древнюю игру го, эти две игры не связаны. Го – старинная китайская игра, она даже упоминается в «Анналах» Конфуция, но на Западе с ней познакомились благодаря японцам, и потому она известна под японским названием.

Пусть я и обрел немалый опыт, играя в «бесконечную» версию «крестиков-ноликов» на нескончаемых уроках или переменах (на переменах веселья меньше, потому что играть разрешено), я все еще не уверен ни в том, есть ли в ней оптимальная стратегия для игрока, который начинает игру (игрок, выбравший «крестики»), ни в том, всегда ли игра заканчивается вничью (то есть не заканчивается никогда), если в нее играют двое сильных игроков. Впрочем, я готов даже заключить пари на то, что выигрышная стратегия существует. Когда я выйду на пенсию и у меня будет много свободного времени, я постараюсь найти ее для игрока, делающего первый ход.

И все-таки, если уж быть честным до конца, я должен сказать, что не играл в «крестики-нолики» уже несколько десятков лет и вспомнил о них, только когда писал эту книгу. А поскольку мои планы на то, чтобы вновь уделить внимание стратегическим аспектам этой игры, рассчитаны на очень долгий срок, прошу – будьте первыми, найдите эту стратегию и сберегите мне время и силы.

Представьте такую ситуацию. Мне дают два конверта с наличными и говорят, что в одном из них денег в два раза больше, чем в другом. Я могу выбрать себе любой, какой хочу, и забрать его.

Предположим, я выбираю конверт, открываю его и нахожу внутри $1000. Поначалу я очень доволен, но потом начинаю гадать: а что же было в другом конверте, который я не выбрал? Конечно, я не знаю. Там могло быть $2000, и тогда я выбрал плохо, или могло быть $500. Уверен, вы понимаете, в чем проблема. Я думаю, думаю, и тут: «Несчастный я человек! Ведь в том, другом конверте потенциальных денег в среднем больше, чем у меня в руках! В конце концов, там либо $2000, либо $500, шансы равны, в среднем это $1250, а это больше, чем $1000. Я свою математику знаю!»

По правде, что бы я ни обнаружил в своем конверте, подтвердится закон Мерфи: «Все, что может пойти не так, пойдет не так». Другой конверт в среднем всегда будет лучше моего. Если я найду в своем конверте $400, в другом будет либо $800, либо $200, а значит, среднее – $500. При таком образе мыслей я никогда не смогу выбрать верно. Выгода в оставшемся конверте всегда будет на 25 % больше моей. Так может, лучше переменить решение – если мне предложат такой вариант, прежде чем я смогу увидеть, что там, в другом конверте? Если я сделаю так, то начну «бесконечную петлю». Но почему такой простой выбор стал столь сложным?

История, которую я вам рассказал, – это знаменитый парадокс, и впервые его представил бельгийский математик Морис Крайчик (1882–1957). Впрочем, его история была о галстуках. Двое спорили о том, чей галстук лучше, и попросили третьего, ведущего галстучного эксперта Бельгии, выступить в роли судьи. Тот согласился, но при условии, что победитель отдаст свой галстук проигравшему в качестве утешительного приза. Владельцы недолго думая согласились, ведь каждый решил: «Не знаю, лучше ли мой галстук. Я могу его лишиться, но могу и приобрести лучший, так что эта игра мне на пользу, как и пари». Как мог каждый из соперников поверить в то, что преимущество на его стороне?

В 1953 г. Крайчик предложил иную версию истории, задействовав в ней двух других поссорившихся бельгийцев. Они галстуков уже не носили, потому что были так набиты бельгийским шоколадом, что едва могли дышать. Вместо этого они спорили о том, сколько денег у другого в кошельке, и решили, что тот, кто окажется богаче и счастливее, отдаст свой бумажник бедному противнику. А если все закончится ничьей, оба вернутся к своим шоколадкам.

Опять же, каждому казалось, что преимущество на его стороне. Если случится потерпеть поражение – что же, отдавать все равно придется меньше, чем может принести победа. Что же это – великая игра или нечто иное? Попытайтесь сыграть в нее на улице со случайными прохожими и посмотрите, что будет. В 1982 г. Мартин Гарднер сделал эту историю популярной в своей книге «А ну-ка, догадайся» [9] Выходила на русском языке в изд-ве «Мир» в 1984 г. – Примеч. ред. [10] С размышлениями Мартина Гарднера об игре 5 можно ознакомиться по книге: Gardner Martin. Aha! Gotcha: Paradoxes to Puzzle and Delight. W. H. Freeman & Co. Ltd, New York, 1982. – одной из самых лучших, самых простых и самых увлекательных из всех самых лучших, самых простых и самых увлекательных книг, когда-либо написанных о проницательности и смекалке.

Барри Нейлбаф (профессор менеджмента на кафедре Милтона Стейнбаха в Йельской школе менеджмента), ведущий специалист по теории игр, в своей статье, опубликованной в 1989 г., предложил версию этой истории с конвертом. Возможно, вы удивитесь, но даже сегодня у этой игры нет решения, с которым были бы единодушно согласны все статистики.

Одно из предлагаемых решений подразумевает, что мы противопоставляем среднее геометрическое и среднее арифметическое. Среднее геометрическое – это квадратный корень из произведения двух чисел. Например, среднее геометрическое 4 и 9 равняется квадратному корню из их произведения (результата перемножения обоих чисел) – а именно 6. Итак, если мы нашли в своем конверте X долларов и знаем, что другой содержал 2 X или ½ X , то среднее геометрическое другого конверта будет равняться X – и в точности соответствовать тому, что попало к нам в руки. Логика применения среднего геометрического опирается на тот факт, что мы говорим не о сложении, а об умножении (вдвое больше). Если бы мы сказали, что в одном конверте на $10 больше, чем в другом, то использовали бы среднее арифметическое, нашли бы его, и никакого парадокса бы не возникло, ведь в нашем конверте содержится X , а в другом – X +10 или X- 10, и среднее количество денег в конверте, который мы не выбрали, равняется X .