Джеффри Уэст - Масштаб. Универсальные законы роста, инноваций, устойчивости и темпов жизни организмов, городов, экономических систем и компаний

Сетевые принципы, лежащие в основе экономии на масштабе и сублинейного масштабирования в биологии, имеют два важных последствия. Они сдерживают темп жизни – крупные животные живут дольше, развиваются медленнее и имеют более низкую частоту сердцебиения, и все это в одной и той же степени, – и ограничивают рост. Напротив, города и экономические системы существуют за счет социальных взаимодействий, механизмы обратных связей которых порождают прямо противоположную картину. Темп жизни систематически увеличивается с ростом численности населения: быстрее распространяются болезни, чаще рождаются и умирают предприятия, и даже люди в крупных городах ходят быстрее, и все эти увеличения приблизительно соответствуют одному и тому же правилу 15 %. Более того, динамика социальных сетей, лежащая в основе суперлинейного масштабирования, порождает неограниченный рост, который является основополагающей чертой современных городов и экономических систем. Здесь господствует не равновесие, но непрерывная адаптация.

У нас получилась замечательно последовательная картина: одна и та же концептуальная система, основанная на фундаментальных сетевых динамике и геометрии с одной и той же математической структурой, приводит в двух разных случаях к двум совершенно разным результатам, и оба этих результата надежно подтверждаются множеством разнообразных данных и наблюдений. Однако здесь есть одно важное обстоятельство, которое может иметь огромные последствия. Хотя рост организмов, городов и экономических систем подчиняется практически одинаковым математическим уравнениям, между получающимися из них решениями существует тонкое, но принципиально важное различие, вызванное тем, что в одном случае действует масштабирование сублинейное (экономия на масштабе у организмов), а в другом – суперлинейное (усиление на масштабе у городов и экономики). В суперлинейном случае общее решение обладает неожиданно нетривиальным свойством, известным под названием сингулярности конечного времени , которая является признаком неизбежных перемен и возможных крупных неприятностей в будущем.

Сингулярность конечного времени означает попросту, что математическое решение уравнения роста, которое управляет рассматриваемой величиной – численностью населения, ВВП, числом патентов и так далее, – в некоторый конечный момент времени становится бесконечно большим , как показано на рис. 76. Это, очевидно, невозможно, и поэтому необходимы какие-то перемены.

Прежде чем мы рассмотрим некоторые последствия этого явления, позвольте мне остановиться на некоторых из его наиболее характерных особенностей. Простые степенные законы порождают экспоненциальный рост и монотонно возрастающие функции, которые тоже в конце концов становятся бесконечно большими, но лишь по прошествии бесконечного времени. Другими словами, моменты «сингулярности» отодвигаются в бесконечно далекое будущее, что делает их «безвредными» по сравнению с сингулярностью конечного времени. В случае роста, вызываемого суперлинейным масштабированием, приближение к сингулярности конечного времени, обозначенной на рис. 76 сплошной линией, опережает экспоненциальный рост. Такой рост часто называют суперэкспоненциальным , и мы уже использовали этот термин, когда говорили о росте городов.

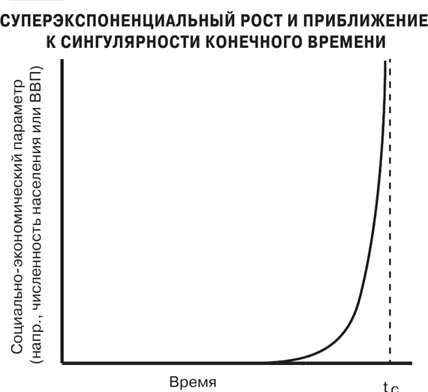
Рис. 76. График, иллюстрирующий сингулярность конечного времени: представленная величина растет суперэкспоненциальным образом и становится бесконечно большой за конечное время t c, обозначенное вертикальной штриховой линией

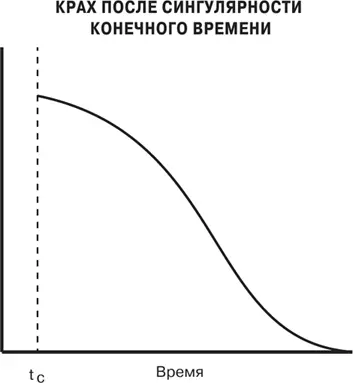
Рис. 77. Иллюстрация застоя и краха, наступающих после сингулярности

Такое поведение явно не может быть устойчивым, так как его поддержание требует неограниченного, постоянно увеличивающегося и в конечном счете бесконечного поступления энергетических и материальных ресурсов за конечное время. Теория предсказывает, что, если его никак не ограничивать, оно должно вызвать переход к фазе, которая приводит к застою и последующему обрушению, как показано на рис. 77. Этот сценарий похож на возрождение мальтузианского тезиса, который отбрасывали целые поколения экономистов: мы не сможем обеспечить удовлетворение потребностей, и неограниченный рост в конце концов приведет к катастрофе.

И это подводит нас к самой сути дела. Наличие сингулярности конечного времени, порожденной суперлинейным масштабированием, радикально отличает этот сценарий от сценария Мальтуса. Если бы рост был чисто экспоненциальным, как предполагали мальтузианцы, неомальтузианцы, их последователи и их критики, то производство энергетических, материальных и пищевых ресурсов могло бы, по меньшей мере в принципе, поспевать за экспоненциальным расширением, так как все существенные характеристики экономики или города остаются конечными, даже если они продолжают расти и становятся очень большими.

Но при суперэкспоненциальном росте и приближении к сингулярности конечного времени это неосуществимо. В этом сценарии потребности все более и более возрастают и в конце концов становятся бесконечными в течение конечного времени. Обеспечение бесконечного количества энергетических, материальных и пищевых ресурсов в течение конечного времени попросту невозможно. Поэтому, если не происходит никаких перемен, этот процесс неизбежно ведет к застою и краху, как показано на рис. 77. Обширный анализ, который выполнили в 2001 г. Дидье Сорнет и Андерс Йохансен, работавшие тогда в UCLA, показал, что данные по росту населения и росту финансовых и экономических показателей убедительно свидетельствуют о наличии суперэкспоненциального роста и, следовательно, движения в направлении такой сингулярности [167].

Я хочу подчеркнуть, что эта ситуация качественно отличается от классической мальтузианской динамики, в которой такой сингулярности не существует. Наличие сингулярности означает неизбежность перехода системы из одной фазы в другую, обладающую существенно иными характеристиками, подобно тому как конденсация пара в воду и последующее ее замерзание в лед являются проявлениями фазовых переходов одной и той же системы между состояниями, обладающими совершенно разными физическими свойствами. И действительно, эти знакомые нам фазовые переходы порождаются сингулярностями термодинамических переменных, описывающих систему (то есть воду), но изменяющихся в зависимости не от времени, а от температуры (с замерзанием при 0 °C и кипением при 100 °C). К сожалению, в случае городов и социально-экономических систем фазовый переход, вызванный сингулярностью конечного времени, – это переход от суперэкспоненциального роста к застою и краху, что может привести к самым гибельным последствиям.