Джеймс Глик - Хаос. Создание новой науки

Освоившись с новым способом исследования фигур при помощи компьютера, Хаббард также решил привнести новый математический стиль мышления и применить для рассмотрения динамических систем методы комплексного анализа, чего раньше не делали. Он чувствовал, что все может быть собрано вместе. Различные разделы математики в определенных местах сходятся воедино. Хаббард также знал, что будет недостаточно лишь увидеть множество Мандельброта. Он хотел добиться полной ясности. В конце концов он заявил, что это ему удалось.

Если бы граница была просто фрактальной – в духе причудливых картин Мандельброта, – тогда каждое последующее изображение более или менее походило бы на предыдущее. Принцип самоподобия при различном масштабировании позволил бы предугадать, что мы увидим в электронный микроскоп на следующем уровне увеличения. Вместо этого каждый взгляд в глубины множества Мандельброта приносил все новые сюрпризы. Желая применить свой термин «фрактал» к новому объекту, Мандельброт начал беспокоиться о том, что определил это понятие слишком узко [292]. При достаточном увеличении выяснилось, что система приблизительно повторяет свои же элементы – крошечные, похожие на жучков объекты, отделявшиеся от основного «тела». Однако, еще больше увеличив изображение, исследователь убеждался, что эти молекулы не во всем соответствуют друг другу – всегда появлялись новые формы, похожие на морских коньков или на вьющиеся ветви оранжерейных растений. Фактически ни один фрагмент системы точно не походил на другой при любом увеличении.

Обнаружение «плавающих» молекул сразу же повлекло за собой дополнительные трудности. Являлось ли множество Мандельброта связным, похожим на континент с выдающимися вперед полуостровами? Или оно походило на рассеянное скопление, где основной объект окружали мелкие островки? Ответ на этот вопрос был далеко не очевидным. Знания о множествах Жюлиа мало что давали, поскольку их графические образы бывают двух разных типов: одни представляют собой целые фигуры, другие смахивают на скопление пылинок. Эти мельчайшие частицы, будучи фрактальными, обладали особым свойством: они не составляли единого целого, каждая была отделена от другой зоной пустого пространства [293]. В то же время ни одна «пылинка» не выглядит обособленной; заметив одну, всегда можно найти и расположенную произвольно близко группу частиц. Разглядывая свои картины, Мандельброт постепенно понимал, что с помощью компьютерного эксперимента ему не удается ответить на основной вопрос. Его внимание сосредоточилось на частичках, «парящих» вокруг основной формы. Некоторые из них пропадали, другие, удивительно похожие, наоборот, появлялись. Казалось, они не зависели друг от друга, но, возможно, были связаны между собой линиями, столь тонкими, что решетка уже найденных точек никак не могла уловить их.

Дуади и Хаббард блестяще использовали свою новую математику, чтобы доказать, что каждая плавающая молекула на самом деле «висит» на филигранной нити, которая связывает ее с другими молекулами. В итоге получается хрупкая паутинка, ведущая от крошечных частиц к основному объекту, – «дьявольский полимер», по словам Мандельброта. Математики доказали, что в каждом сегменте – не имеет значения, где он находится и насколько он мал, – при увеличении «компьютерным микроскопом» обнаружатся новые молекулы, каждая из которых будет напоминать систему в целом и одновременно отличаться от нее. Каждая новая молекула будет обладать собственными спиралями и выступающими частями, похожими на языки пламени, и в них также неизбежно обнаружатся новые молекулы, еще меньшие, всегда подобные, но никогда – полностью идентичные, словно следующие предписанию о бесконечном разнообразии. Это можно назвать чудом миниатюризации: каждая новая деталь является вселенной, цельной и многоликой.

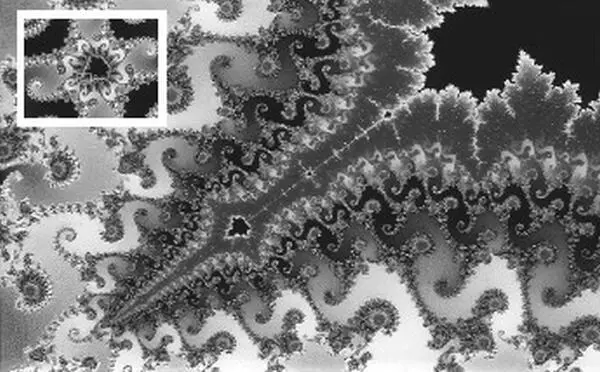
Фракталы Мандельброта.

«Все в высшей степени геометрическое, причем преобладают решения, продиктованные прямыми линиями, – сказал Хайнц-Отто Пайтген, рассуждая о современном искусстве. – В частности, творения Джозефа Альберса, пытавшегося истолковать соотношение цветов, в сущности являли собой квадраты различных оттенков, размещенные один на другом. Такие вещи пользовались большой популярностью, но сейчас, взглянув на них, мы понимаем, что их время миновало. Людей такое уже не привлекает. В Германии строятся огромные жилые кварталы в стиле баухаус, но все выезжают оттуда, никто не желает в них жить. Как мне кажется, общество сегодня имеет веские причины для настороженного отношения к некоторым нашим взглядам на природу» [294]. Пайтген помогал посетителям выбирать увеличенные изображения некоторых участков множества Мандельброта, множеств Жюлиа и других итерационных процессов, оформленные в изысканной цветовой гамме. В своем небольшом кабинете в Калифорнии он демонстрировал слайды, огромные плакаты и даже календарь с изображением множества Мандельброта. «Эта изменившаяся перспектива взгляда на окружающий мир вызывает огромный энтузиазм. Какой взгляд на природный объект верный? Скажем, что важнее всего в дереве? Прямая ли это линия или фрактальный образ?» Тем временем в Корнелле Джону Хаббарду пришлось столкнуться с коммерческими реалиями [295]. Когда математический факультет одолели сотнями просьб выслать изображения системы Мандельброта, он понял, что должен подготовить образцы и составить что-то вроде прейскуранта. В его вычислительных машинах хранились десятки уже просчитанных объектов, готовых к немедленной демонстрации. Организовать показ ему помогали аспиранты, помнившие все технические детали. Но все же наиболее эффектные картины, отпечатанные с большим разрешением и ярко расцвеченные, распространяли двое немцев – Пайтген и Петер Рихтер, трудившиеся вместе с группой ученых в Бременском университете при надежной поддержке одного из местных банков.

Пайтген и Рихтер – математик и физик – обратились в своих исследованиях к множеству Мандельброта, которое стало для них кладезем идей, питавших современную философию искусства, оправданием новой роли эксперимента в математике, а также средством популяризации сложных систем. Они опубликовали множество сверкавших глянцем каталогов и книг, которые показали всему миру галерею компьютерных образов. Рихтер пришел к изучению сложных систем из физики, через химию, а затем и биохимию, где изучал биологические осцилляции [296]. В серии статей, посвященных иммунной системе и окислению глюкозы, он сообщал, что колебания часто управляют динамикой процессов, которые традиционно рассматривались как статические по причине того, что живые системы не так-то легко изучать в режиме реального времени. Рихтер прикрепил к своему подоконнику хорошо смазанный двойной маятник, «комнатную динамическую систему», сконструированную по его заказу в университетской мастерской. Время от времени ученый запускал систему, задавая хаотические неритмичные движения, которые он мог имитировать также и с помощью компьютера. Зависимость от начальных условий оказалась настолько сильной, что гравитационное притяжение единственной дождевой капли в миле от места проведения опыта спутывало движение в пределах пятидесяти-шестидесяти полных оборотов, что занимало около двух минут. Многоцветные графические рисунки Рихтера, где изображалось фазовое пространство его маятника, указывали на зоны смешения периодичности и хаоса. Ученый использовал аналогичную графическую технику для изображения идеализированных участков намагничивания в металле, а также для изучения множества Мандельброта.