Чарльз Петцольд - Код. Тайный язык информатики

3725ВОСЕМЬ = 3 × 1000ВОСЕМЬ +

7 × 100ВОСЕМЬ +

2 × 10ВОСЕМЬ +

5 × 1.

А можно сделать вот так:

3725ВОСЕМЬ = 3 × 83 +

7 × 82 +

2 × 81 +

5 × 80.

Если выполнить эти расчеты в десятеричной системе, получится 2005ДЕСЯТЬ. Таким образом восьмеричные числа преобразуются в десятеричные.

Восьмеричные числа складываются и перемножаются в точности как десятеричные. Разница в том, что таблицы умножения и сложения для восьмеричных чисел строятся иначе. Вот таблица сложения восьмеричных чисел.

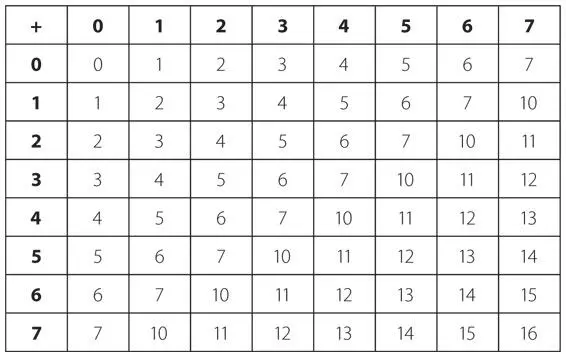
Например, 5ВОСЕМЬ + 7ВОСЕМЬ = 14ВОСЕМЬ, то есть восьмеричные числа можно складывать в столбик.

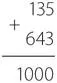
Начинаем справа: 5 плюс 3 равно 10, 0 пишем, 1 в уме; 1 плюс 3 плюс 4 равно 10, 0 пишем, 1 в уме; 1 плюс 1 плюс 6 равно 10.

Аналогично дважды два и в восьмеричной системе равно четырем. Но трижды три не равно девяти. А как? Трижды три равно 11ВОСЕМЬ, это столько же, сколько и 9ДЕСЯТЬ. Далее полностью приведена восьмеричная таблица умножения.

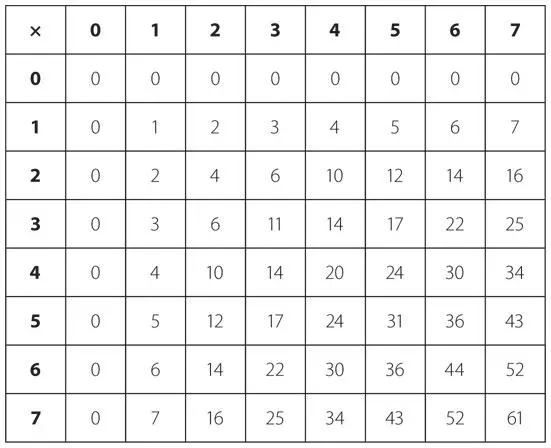
Здесь у нас 4 × 6 равно 30ВОСЕМЬ, но 30ВОСЕМЬ равно 24ДЕСЯТЬ, то есть 4 × 6 в десятеричной системе.

Восьмеричная система счисления столь же полноценна, как и десятеричная.

Мы разработали систему счисления для мультяшек. Теперь давайте создадим такую же систему для омаров. У омаров нет пальцев, но на кончиках передних лап у них клешни. Омарам подойдет четверичная система счисления с основанием четыре.

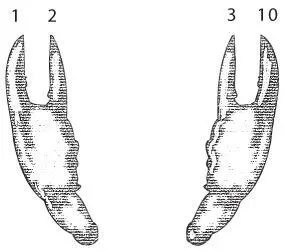
Вот как считают в четверичной системе: 0, 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33, 100, 101, 102, 103, 110 и т. д.

Не буду подробно останавливаться на четверичной системе, поскольку мы приближаемся к более важному вопросу. Как видите, здесь каждая позиция в числе соответствует степени четверки.

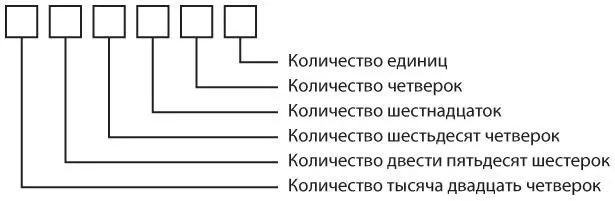
В четверичной системе счисления число 31 232 можно записать следующим образом:

31 232ЧЕТЫРЕ = 3 × 256ДЕСЯТЬ +

1 × 64ДЕСЯТЬ +

2 × 16ДЕСЯТЬ +

3 × 4ДЕСЯТЬ +

2 × 1ДЕСЯТЬ.

Что равнозначно записи:

31 232ЧЕТЫРЕ = 3 × 10 000ЧЕТЫРЕ +

1 × 1000ЧЕТЫРЕ +

2 × 100ЧЕТЫРЕ +

3 × 10ЧЕТЫРЕ +

2 × 1ЧЕТЫРЕ.

А это то же самое, что и:

31 232ЧЕТЫРЕ = 3 × 44 +

1 × 43 +

2 × 42 +

3 × 41 +

2 × 40.

Если мы выполним вычисления в десятичной системе счисления, то обнаружим, что 31 232ЧЕТЫРЕ — это 878ДЕСЯТЬ.

Теперь мы сделаем еще один прыжок, на этот раз окончательный. Представьте, что мы дельфины и можем использовать для подсчета два плавника. В данном случае мы имеем дело с системой счисления с основанием 2, или двоичной , или, иначе, бинарной (от лат. binary — « двойной», «состоящий из двух частей»). Понятно, что у нас будет только две цифры: 0 и 1.

С нулем и единицей мало что можно сделать, и, чтобы привыкнуть к двоичным числам, требуется практика. Проблема в том, что сразу заканчиваются цифры. Например, на следующем рисунке показано, как дельфин считает на плавниках.

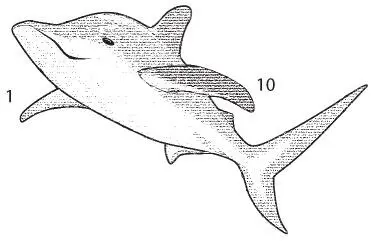
Да, в двоичной системе счисления за 1 следует 10. Это странно, однако это не должно удивлять. Независимо от того, какую систему счисления мы используем, всякий раз, когда у нас заканчиваются отдельные цифры, первое двузначное число всегда 10. В двоичной системе счисления мы считаем:

0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…

Эти числа могут показаться большими, но на самом деле это не так. Скорее, двоичные числа очень быстро становятся длинными , а не большими.

Количество голов у людей — 1ДЕСЯТЬ, или 1ДВА.

Количество плавников у дельфинов — 2ДЕСЯТЬ, или 10ДВА.

Количество чайных ложек в столовой ложке — 3ДЕСЯТЬ, или 11ДВА.

Количество сторон у квадрата — 4ДЕСЯТЬ, или 100ДВА.

Количество пальцев на одной человеческой руке — 5ДЕСЯТЬ, или 101ДВА.

Количество конечностей у насекомых — 6ДЕСЯТЬ, или 110ДВА.

Количество дней в неделе — 7ДЕСЯТЬ, или 111ДВА.

Количество музыкантов в октете — 8ДЕСЯТЬ, или 1000ДВА.

Количество планет в Cолнечной системе, включая Плутон, — 9ДЕСЯТЬ, или 1001ДВА.

Количество центнеров в тонне — 10ДЕСЯТЬ, или 1010ДВА.

В двоичном числе, состоящем из большого количества цифр, позиции знаков соответствуют степени двойки.

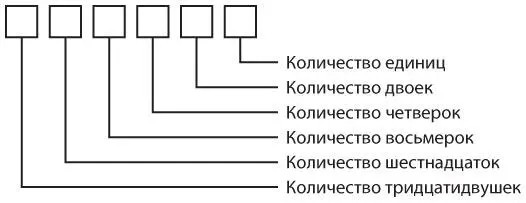
Таким образом, каждый раз, когда встречаем двоичное число, состоящее из единицы и следующих за ней нулей, мы понимаем, что это число соответствует какой-либо из степеней двойки. Эта степень равна количеству нулей в этом двоичном числе. Вот наша расширенная таблица степеней двойки, демонстрирующая такое правило.

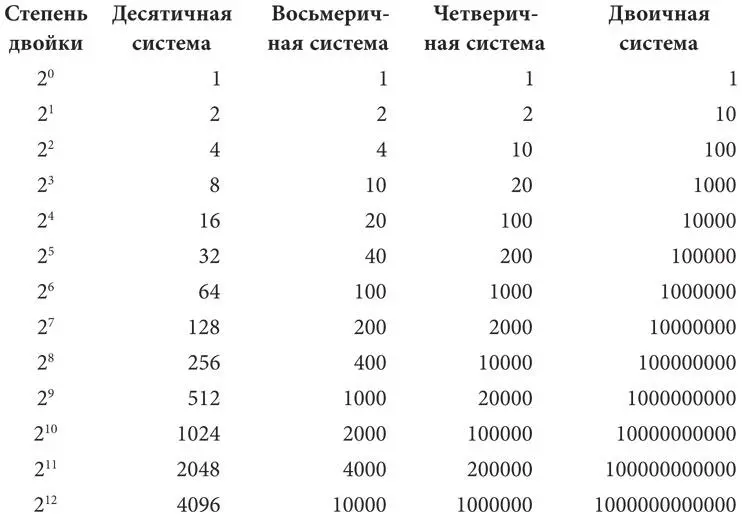
Допустим, у нас есть двоичное число 101101011010. Его можно записать так:

101101011010ДВА = 1 × 2048ДЕСЯТЬ +

0 × 1024ДЕСЯТЬ +

1 × 512ДЕСЯТЬ +

1 × 256ДЕСЯТЬ +

0 × 128ДЕСЯТЬ +

1 × 64ДЕСЯТЬ +

0 × 32ДЕСЯТЬ +

1 × 16ДЕСЯТЬ +

1 × 8ДЕСЯТЬ +

0 × 4ДЕСЯТЬ +

1 × 2ДЕСЯТЬ +

0 × 1ДЕСЯТЬ.

Или:

101101011010ДВА = 1 × 211 +

0 × 210 +

1 × 29 +

1 × 28 +

0 × 27 +

1 × 26 +

0 × 25 +

1 × 24 +

1 × 23 +

0 × 22 +

1 × 21 +

0 × 20.

Если просто сложить все слагаемые в десятичной системе, получим 2048 + 512 + 256 + 64 + 16 + 8 + 2, что составляет 2906ДЕСЯТЬ.

Для более легкого преобразования двоичных чисел в десятичные можно использовать следующую схему.

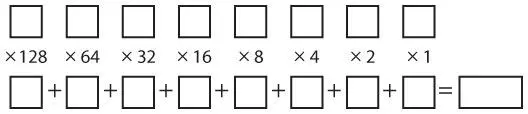
Эта схема позволяет конвертировать числа, содержащие до восьми двоичных разрядов; ее можно легко расширить. Введите до восьми цифр в восемь верхних полей, по одной цифре в каждый квадрат. Выполните восемь операций умножения и введите их результаты в восемь нижних полей. Сложите числа в этих восьми полях для получения окончательного результата. Этот пример демонстрирует процесс нахождения десятичного эквивалента двоичного числа 10010110.

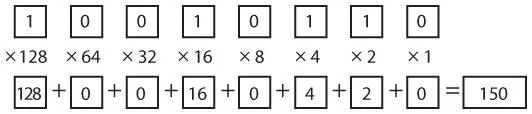
Преобразовать десятичные числа от 0 до 255 в двоичные не так просто, однако вы можете использовать следующую схему.

Процесс преобразования сложнее, чем кажется, поэтому внимательно следуйте указаниям. Поместите десятичное число (меньшее или равное 255) в верхний левый квадрат. Разделите это число (делимое) на первый делитель (128), как показано на схеме. Поместите целую часть в нижнее поле (левый нижний квадрат), а остаток от деления — в поле справа (второй квадрат в верхнем ряду). Этот первый остаток является делимым, которое будет участвовать в следующей операции деления, где в качестве делителя используется число 64.