Сергей Попов - Все формулы мира

С подачи Ксении я начал размышлять над тем, что можно было бы показать на такой выставке, какие мысли передать зрителям. Как, с одной стороны, отразить это «магическое» восприятие, а с другой – разоблачить его. Последующие разговоры, в том числе с художниками, привели к дальнейшему развитию сюжета. Выписывание всего этого (поскольку некоторые диалоги шли через обмен электронными письмами) с пояснениями и сопутствующими рассуждениями привело в конце концов к появлению небольшой книги. Получились своего рода «пролегомены ко всякой будущей выставке о роли математики в современной науке». Отчасти следуя советам тех, кто видел разные отрывки черновика или с кем я обсуждал идею книги, я добавил к основному повествованию приложения, в которых примеры применения математических методов в физике и астрофизике излагаются также и на уровне формул, включая выводы некоторых из них.

Однако словесный (и даже «формульный») рассказ, выросший из обсуждения визуальных образов, был бы неполон без иллюстративной части. При этом было важно, чтобы это были не графики и поясняющие схемы, а самостоятельные художественные произведения. К счастью, к проекту подключился отличный художник Ростан Тавасиев, с которым мы уже сотрудничали, но совсем в других форматах, что в конечном счете позволило создать книгу такой, какой вы ее видите. Обсуждения с Ростаном также помогли мне лучше понять и выразить некоторые из идей и аналогий, представленных в этой книге.

По ходу развития проекта я показывал черновики и обсуждал их с коллегами и знакомыми. Среди них были и художники, и журналисты, и ученые. Особенно я хотел бы поблагодарить математика Николая Андреева и астронома Геннадия Ширмина.

Огромная благодарность научному редактору книги Игорю Иванову, который не только нашел несколько серьезных неточностей в первоначальном варианте рукописи, но и сделал ряд полезных замечаний и комментариев, способствовавших улучшению книги (а также просто расширявших мой кругозор).

Пробные версии некоторых глав и приложений публиковались в газете «Троицкий вариант – Наука». Я признателен коллективу издания и персонально Максиму Борисову и Алексею Огнёву за подробные комментарии, а читателям – за отзывы.

Если ввести величину, равную важности физического закона, деленную на сложность формулы, то закон Хаббла будет среди лидеров, а может быть, займет первое место. В самом деле, он выражает один из самых грандиозных процессов – расширение вселенной. С другой стороны, это просто линейное уравнение, связывающее всего лишь две величины – скорость удаления объектов друг от друга с расстоянием между ними – с помощью так называемой постоянной Хаббла. Итак, v = rH !

Эдвин Хаббл выявил это соотношение из наблюдений. Но, что важно, оно следует и из (относительно) простых теоретических рассуждений. Для этого нам надо задать характеристики нашего пространства-времени. Это делается с помощью метрики. Ее можно представить как некоторую математическую структуру – так называемый интервал (точнее, нам понадобится квадрат интервала), определяемую для двух очень близких точек. Хитрость в том, чтобы выбрать такую структуру, которая не зависела бы от способов измерения, т. е. была так называемым инвариантом.

Начнем с метрики Фридмана – Робертсона – Уокера. Она соответствует однородной изотропной вселенной (т. е. миру, где все направления равноценны и в каждый момент времени свойства везде идентичны). Это самый естественный выбор предположений о глобальных свойствах нашего мира. Кроме того, все наблюдения пока подтверждают его: не обнаружено ни выделенных направлений, ни неоднородностей на больших масштабах (сравнимых с размером видимой части вселенной).

В общем случае метрика записывается для искривленного пространства, но мы выпишем формулу для плоской вселенной – не только потому, что она проще, а еще и потому, что в пределах точности измерений кривизна вселенной равна нулю. «Плоскостность» нашего мира, в частности, говорит о том, что в больших масштабах можно пользоваться евклидовой геометрией (при этом, разумеется, пространство трехмерно).

Сделаем еще одно упрощение при записи метрики. В общем случае в него должны входить три пространственные координаты. Удобно взять не декартову тройку x, y, z , а радиальную и две угловые координаты. Но нас будут интересовать лишь радиальные движения (например, галактика или удаляется от нас, или приближается к нам, но не смещается по небесной сфере), так что угловые координаты мы отбросим. В итоге получается очень простое выражение для квадрата интервала:

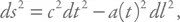
где c – скорость света, dt – временной интервал, dl – элемент длины. Изменяющаяся со временем величина a(t) называется масштабным фактором, она характеризует изменение интервала длины, который мы обозначим dr .

Итак, расстояние между двумя очень близкими точками записывается как dr = adl . Чтобы получить расстояние r между двумя реальными объектами, нам надо интегрировать:

Введем еще одно обозначение: так называемые сопутствующие координаты. Их особенность в том, что они не меняются по мере расширения. Пусть два объекта имеют сопутствующие координаты χ 1и χ 2, тогда соответствующее сопутствующее расстояние χ = χ 1– χ 2остается постоянным, если мы пренебрегаем так называемым пекулярным движением объектов относительно друг друга, связанным, например, с их взаимным гравитационным притяжением.

Определяя r в какой-то момент времени, мы можем считать масштабный фактор a постоянной величиной (ведь он изменяется только со временем и в каждый момент один и тот же для всей вселенной). Значит,

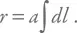
А интеграл от dl равен, по определению, сопутствующему расстоянию:

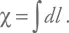
Расстояние r называют собственным. Именно оно показывает, сколько сантиметров (метров, километров, парсек или световых лет) между двумя объектами в данный момент времени. Это расстояние растет в расширяющейся вселенной, что описывается изменением масштабного фактора. Обычно удобно считать, что в настоящий момент a = 1. Соответственно, в прошлом a < 1, а в будущем a > 1.

Теперь, введя все необходимые величины, переходим к выводу закона Хаббла. Определим скорость как производную от собственного расстояния: