Сергей Попов - Все формулы мира

Начнем с оценки давления в центре Солнца (а затем получим температуру, правда, уже не методом размерностей, а используя физику 10-го класса средней школы). Солнце находится в состоянии гидростатического равновесия. Градиент давления (оно растет внутрь) уравновешивает силу тяжести. Значит, давление должно выражаться через параметры, связанные с солнечной гравитацией. Таким образом, в нашу формулу войдет масса Солнца M и гравитационная постоянная G . Сила гравитации зависит от расстояния. Характерный масштаб в задаче – размер Солнца, R . Добавим и его. Тогда для давления получим:

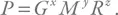
Теперь займемся размерностями. С массой и радиусом все просто: [ M ] = г, [ R ] = см. Давление – это в первую очередь плотность энергии, т. е. для него можно записать:

Размерность энергии, выраженную через базовые величины, можно вспомнить благодаря формуле E = mv 2/ 2: [ E ] = г см 2с –2. Значит, для давления получим: [ P ] = г см –1с –2. Остается гравитационная постоянная. Ее размерность, конечно, можно взять из справочника, а можно вспомнить закон всемирного тяготения:

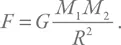
Для размерностей должно выполняться такое же соотношение:

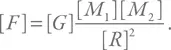
Иначе говоря, [ G ] = [ F ][ R ] 2/ [ M ] 2. Размерность силы (напомним, что сила равна произведению массы на ускорение) равняется г см с –2. Значит, [ G ] = г см с –2см 2г –2= г –1см 3с –2. Теперь можно вернуться к нашему уравнению для давления, записав его для размерностей:

г см –1с –2= (г –1см 3с –2) x (г) y (см) z .

Преобразуем правую часть и упорядочим ее, получим:

г см –1с –2= г y – x см 3 x + z с –2 x .

По отдельности должны выполняться равенства для каждой базовой размерности слева и справа, т. е. имеем систему уравнений: 1 = y – x; –1 = 3 x + z; – 2 = –2 x .

Решая ее, получим: x = 1; y = 2; z = –4.

Иначе говоря, P = GM 2 R –4. Это то, что мы и хотели! Формула для расчета давления в недрах Солнца!!! Остается подставить солнечную массу (2·10 33г) и радиус (696 000 км). Получим, что давление в центре Солнца в 10 млрд раз больше атмосферного давления у поверхности Земли!

Чтобы получить температуру, возьмем формулу для идеального газа из школьного учебника:

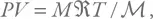
где V – объем, 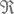– универсальная газовая постоянная, а 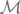– молярный вес (для простоты можно считать, что Солнце состоит из атомарного водорода). Вместо давления подставим P = GM 2 R –4и преобразуем формулы, выразив температуру:

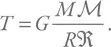
Остается подставить числа. Ответ – температура порядка 20 млн Кельвин. Полученные нами оценки температуры и давления близки к верным значениям.

Аналогично можно получить формулу для периода пульсаций звезды. Правда, здесь ответ будет менее точным из-за наличия безразмерного коэффициента, который нам трудно определить точно таким же методом. Зато зависимость от ключевых величин мы получим правильную.

Снова будем искать формулу для периода в виде G xM yR z . Есть всего лишь один набор показателей степени x, y, z , дающих величину с размерностью времени. Эта комбинация: R 3 / 2/ ( GM ) 1 / 2. Заметим, что частное от деления массы на куб радиуса имеет размерность плотности. Тогда получим, что период пульсаций звезды (вообще, газового шара), P puls , пропорционален квадратному корню из произведения гравитационной постоянной на среднюю плотность. А поскольку G – постоянная, то важным фактом является пропорциональность периода пульсаций обратному квадратному корню из плотности:

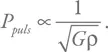
У звезд типа Солнца чем меньше масса, тем выше средняя плотность. Это говорит о том, что с ростом массы растет и период пульсаций. Кроме того, низкая средняя плотность проэволюционировавших и раздувшихся звезд приводит к большим периодам, что и наблюдается. Если у Солнца основной период пульсаций составляет около часа, то у звезд-гигантов он может составлять десятки дней, что неудивительно, ведь их радиусы в сотни раз больше.

Возьмем предмет, поднимем его над полом и отпустим. Он со стуком упадет. Звук – это продольные волны, распространяющиеся в среде и переносящие энергию. Откуда взялась эта энергия в случае падающего тела? Ответ дается в школьном курсе физики. Там рассказывается, что тело на высоте h имеет так называемую потенциальную энергию E p = mgh , где m – масса тела, а g – ускорение свободного падения. Ускорение можно рассчитать из закона всемирного тяготения:

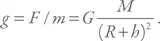
где G – ньютоновская постоянная, M – масса Земли, а R – ее радиус.

В школьных задачах чаще всего можно считать, что высота, с которой падает тело, намного меньше радиуса Земли ( R >> h ), поэтому g не изменяется.

При падении тело разгоняется, так как на него действует сила в направлении движения. Растет кинетическая энергия, равная:

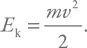
Этот рост происходит за счет уменьшения потенциальной энергии. К моменту удара, как учит нас школьный учебник, вся потенциальная энергия успела перейти в кинетическую. Затем практически мгновенно вся кинетическая энергия перейдет в другие формы, например в тепловую энергию и в энергию звуковой волны. В бытовых ситуациях тепловой эффект мы обычно не замечаем, но вот если на Землю падает крупный метеорит, то нагрев более чем заметен, свидетельством чего являются так называемые тектиты – оплавленные куски стекла, возникающие из-за нагрева пород при ударе.

Школьное описание является несколько упрощенной версией. Нас будет интересовать падение вещества на нейтронные звезды и черные дыры, при этом расстояние, с которого оно прилетает, намного больше размеров компактных объектов. Для такого случая запишем потенциальную энергию более корректно:

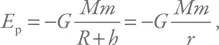
где M – масса массивного тела, а m – масса падающего объекта (в такой постановке M >> m ).