Сергей Попов - Все формулы мира

Поскольку сила действует на электрон, то в качестве площади возьмем так называемое томсоновское сечение, σ T. По сути, это эффективная площадь электрона при рассеянии на нем электромагнитных волн. Точная формула такова:

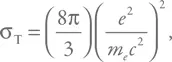
где m e – масса электрона, а e – его заряд.

Величину e 2/m ec 2 называют классическим радиусом электрона.

Итак, мы знаем площадь, как теперь оценить давление? Очень просто. Давит излучение. Давление же характеризуется плотностью энергии, т. е. нам надо оценить плотность энергии излучения. Мы знаем поток, или сколько энергии проходит в единицу времени через единичную площадь. Плотность энергии будет равна потоку, деленному на длину, проходимую излучением за единицу времени. Длина равна произведению скорости (в нашем случае это скорость света) на время (т. е. на единицу, так как мы рассматриваем единичный интервал). Для давления получаем: I / c . А для силы:

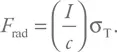
Из равенства F grav= F radполучим:

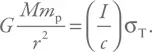
Подставим выражение для I , и тогда:

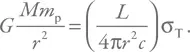
Видим, что равенство не зависит от расстояния. Выражаем светимость (и вводим обозначение L Edd):

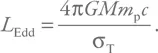
Подставляя характерные значения и константы, получим:

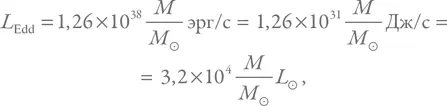
где L ʘ – солнечная светимость, а M ʘ – масса Солнца.

Таким образом, для каждой массы центрального объекта (будь то обычная звезда или нейтронная, черная дыра звездной массы или сверхмассивная) есть предельная светимость. Мы рассматривали сферически симметричную геометрию, отклонения от нее могут немного увеличить предельную светимость. Если рассмотреть не чисто водородную плазму, то мы также получим несколько иной результат. Тем не менее предел есть, и он работает.

Наличие предельной светимости позволяет делать оценки массы центральных объектов. Например, если в центре какой-то галактики мы наблюдаем активное ядро, то его светимость позволяет дать нижний предел на массу сверхмассивной черной дыры. И наоборот, знание о диапазоне масс сверхмассивных черных дыр позволяет предсказать диапазон их светимостей. В типичных квазарах массы центральных объектов составляют десятки миллионов солнечных. Значит, светимости квазаров не должны превосходить примерно несколько триллионов светимостей Солнца.

Наконец, ответим еще на один вопрос. В каком диапазоне будет излучать аккрецирующая нейтронная звезда при светимости, близкой к предельной? Это легко оценить. В данном случае можно предположить, что вся поверхность компактного объекта (и/или внутренняя часть аккреционного диска, чья площадь по порядку величины близка к полной площади поверхности нейтронной звезды) нагрета до определенной температуры и излучает так называемое абсолютно черное тело. В таком случае светимость равна:

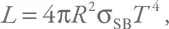
где σ SB – постоянная Стефана – Больцмана.

Подставив эддингтоновскую светимость и радиус нейтронной звезды 10 км, получим, что температура составляет порядка 20 млн Кельвин. Такая температура соответствует рентгеновскому излучению, поэтому нейтронные звезды в тесных двойных системах с большим темпом аккреции мы наблюдаем именно как рентгеновские источники.

Черные дыры, безусловно, являются крайне интригующими объектами, ускользающими не только от однозначной идентификации наблюдательными методами, но еще и от четкого определения [99] О проблеме определения понятия черная дыра см. статью Эрика Кьюриэла (Eric Curiel) в журнале Nature Astronomy (т. 3, с. 27–34). Эта работа также доступна в Архиве электронных препринтов под номером 1808.01507. В этой публикации представлены точки зрения множества физиков и астрономов на то, как следует правильно формулировать ключевые свойства черных дыр. Разумеется, разные ученые (работающие в разных областях) дают сильно отличающиеся определения, что в первую очередь отражает различные подходы к проблеме. . Тем не менее в астрофизике существует несколько методов, позволяющих регистрировать даже одиночные черные дыры звездных масс. Какие-то из них уже работают, какие-то – только на подходе. Ниже мы обсудим три ситуации: аккрецию вещества межзвездной среды, гравитационное микролинзирование и, наконец, испарение черных дыр (хотя этот процесс важен лишь для черных дыр малых масс).

Ядра массивных звезд в завершение их эволюции могут превращаться в черные дыры. Точные интервалы начальных масс прародителей этих компактных объектов неизвестны, но для простой оценки предположим, что основная доля звезд, имеющих при рождении массы более 30 солнечных, в конце порождают именно черные дыры [100] В действительности существует несколько диапазонов масс звезд-прародителей, которые при разных условиях заканчивают свою эволюцию как черные дыры. Некоторые из них делают это без взрыва сверхновой, а некоторые – со взрывом. . Далее предположим, что распределение звезд по начальным массам можно описать так называемой солпитеровской функцией [101] Эта функция масс была предложена Эдом Солпитером (Ed Salpeter) в 1953 г. и является наиболее популярным простым способом описать так называемую начальную функцию масс звезд. :

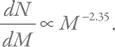
Это означает, что количество звезд dN в небольшом интервале масс шириной dM – от M до ( M + dM ) – пропорционально массе в степени –2,35, т. е. количество звезд быстро спадает с ростом массы [102] Уменьшение числа звезд при росте массы – надежно установленное свойство. А вот конкретный вид функции может зависеть от ряда факторов (от массы, от химического состава и т. д.). Тем не менее солпитеровская функция остается хорошим первым приближением. . Данная зависимость была установлена на основе наблюдений.

В качестве минимальной массы звезды возьмем 0,1 M ʘ, а в качестве максимальной – 100 M ʘ. Теперь, чтобы посчитать долю звезд с массой более 30 солнечных, нам надо найти отношение двух интегралов: