Сергей Попов - Все формулы мира

Какие эффекты могут возникать при таком пролете? Во-первых, это просто смещение видимого положения звезды-источника. Такой случай называют астрометрическим линзированием . Наблюдать эффект очень трудно, так как он мал. Но иногда это удается (если знать, куда смотреть с помощью крупных телескопов), а кроме того, спутник Gaia вскоре должен представить много данных по таким явлениям. Но более известным является так называемое фотометрическое микролинзирование , к которому мы и перейдем.

Гравитационная линза всегда работает таким образом, что усиливает блеск источника. Для этого он должен оказаться на небольшом угловом расстоянии от линзы – внутри так называемого конуса Эйнштейна . Если считать, что источник расположен гораздо дальше линзы, то этот кружок на небе характеризуется угловым радиусом, вычисляемым по очень простой формуле (вот только вывод ее не так уж прост, и здесь мы его приводить не будем):

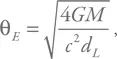
где d L – расстояние от наблюдателя до линзы, а М – ее масса.

Если подставить звездную массу и расстояние порядка нескольких тысяч световых лет, то мы получим угол примерно в несколько сотых угловой секунды. Вероятность того, что одна из звезд попадет в такой кружок, крайне мала, поэтому и надо ждать сотни тысяч лет, пока это произойдет. Но если уж такое случилось, то блеск звезды возрастает в несколько раз, что легко заметить.

С появлением цифровых приемников излучения, чья главная характеристика – число мегапикселей, астрономы научились сразу измерять блеск большого числа звезд. Это дало возможность начать специальные программы наблюдений, охотящихся за случаями микролинзирования. Сейчас счет зарегистрированным событиям идет на многие тысячи.

А что же черные дыры? Насколько часто в роли линзы может выступить такой объект? Чтобы в этом разобраться, нам надо сравнить количество и массы обычных звезд, черных дыр, а также нейтронных звезд и белых карликов [107] Познакомиться с гораздо более детальными расчетами можно в статье Николо Сарторе и Альдо Тревеса Probing isolated compact remnants with microlensing, опубликованной в журнале Astronomy and Astrophysics , 523, id. A33 (2010), и статье Хироко Ниикура с соавторами Constraints on Earth-mass primordial black holes from OGLE 5-year microlensing events, опубликованной в журнале Physical Review D , 99, id. 083503. .

Начнем с масс. Наблюдения говорят нам, что средняя масса белых карликов составляет примерно 0,6 солнечных, нейтронных звезд – 1,3, а черных дыр – 5–10. Для обычных звезд мы снова воспользуемся начальной функцией масс в виде:

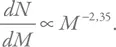
Масса звезд в интервале dM в окрестности какой-то массы M равна просто произведению этой массы на dN . Соответственно, полная масса звезд будет пропорциональна интегралу

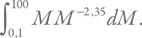
А полное количество звезд, как и выше в приложении 4А, – интегралу

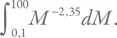
Коэффициент пропорциональности одинаковый. Соответственно, средняя масса звезды, равная отношению массы всех звезд к их количеству, будет отношением этих интегралов. Учитывая, что нижний предел гораздо меньше верхнего, а под интегралом стоят отрицательные степени, по модулю большие единицы, мы получим, что отношение примерно равно 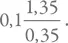. Это дает 0,38. Обычно используется средняя звездная масса, равная 0,3, поскольку в качестве нижнего предела подставляется неокругленное значение 0,08 солнечных масс.

Итак, звезды в среднем вдвое легче белых карликов, примерно в пять раз – нейтронных звезд и примерно в 20 раз – черных дыр. Это важно, так как для этих объектов будут пропорционально квадратному корню из массы изменяться параметры конусов Эйнштейна.

Теперь оценим относительное количество этих четырех типов объектов. Выше, в приложении 4А, мы уже сравнивали количество черных дыр с количеством звезд. Аналогичным способом, меняя пределы интегралов, можно получить, что нейтронных звезд примерно в 5 раз, а белых карликов раз в 20 больше, чем черных дыр.

Собирая все вместе, получаем, что почти 90 % случаев линзирования должны быть связаны с обычными звездами [108] Здесь мы не учитываем вклад бурых карликов, который, вообще говоря, немал и может превосходить вклад белых карликов. Можно считать, что в оценках мы приплюсовали бурых карликов к обычным звездам, которым они заметно уступают по вкладу в линзирование. . Примерно в 10 % случаев линзами могут являться белые карлики, а вот на долю нейтронных звезд и черных дыр вместе приходится около 1–2 % (вклад нейтронных звезд несколько уменьшается из-за их высокой скорости, так как они быстро покидают диск Галактики). Однако, поскольку случаев линзирования известно уже более десяти тысяч, то и 1 % – это хорошо.

В самом деле, на сегодняшний день выявлено более десятка случаев линзирования, где линзой является нейтронная звезда или черная дыра. Здесь первый шаг таков. Данные наблюдений позволяют получить распределения вероятностей для массы линзы и расстояния до нее. Затем мы можем попытаться увидеть объект, выступивший в роли линзы. При типичных массах нейтронных звезд и черных дыр это были бы довольно заметные звезды. Таким образом, если ничего не удается увидеть, то это сильный аргумент в пользу того, что мы имеем дело именно с компактным объектом, а не с обычной звездой.

На втором шаге нам надо попробовать различить нейтронные звезды и черные дыры. И тут подход очень прост. Если масса темной линзы превосходит три солнечных, то объект считают черной дырой. На сегодняшний день выявлено несколько таких кандидатов. Из-за значительной массы черных дыр и их относительно небольшой скорости продолжительность событий линзирования на таких объектах весьма велика – обычно более года! Так что времени для детального построения кривой блеска источника предостаточно. Проблема в том, что мы не можем изучать, не можем (пока?) никаким способом идентифицировать черную дыру по окончании эпизода линзирования. Поэтому часть коллег считают, что все такие кандидаты недостаточно надежны. Тем не менее на сегодня это единственный, хоть как-то работающий способ получать прямую информацию об одиночных черных дырах звездных масс.

Одним из самых потрясающих открытий, которые к тому же могут произойти в любой момент (надо только много-много везения), было бы обнаружение испарения черных дыр. Это не только доказало бы существование хокинговского излучения, не только стало бы самым надежным доказательством существования черных дыр, но вдобавок дало бы нам в руки уникальный инструмент по проверке моделей квантовой гравитации.