Сергей Попов - Все формулы мира

Как мы увидим в дальнейшем, только очень легкие черные дыры могут дойти до финальных стадий испарения за 13–14 млрд лет – время жизни вселенной. В настоящее время испаряются черные дыры, имевшие вначале массы порядка 10 15г, а черные дыры тяжелее 10 26г (это примерно масса Луны) вообще наращивают массу, а не уменьшают ее. Откуда же берутся такие черные дыры?

Еще в конце 1960-х гг. начали обсуждать возможность рождения черных дыр в молодой вселенной, когда плотность вещества была очень велика (одними из первых такие идеи высказали Яков Зельдович и Игорь Новиков). А начиная с 1970-х гг. благодаря трудам Стивена Хокинга и других ученых эта идея стала весьма популярной гипотезой, в верности которой сейчас мало кто сомневается.

Сама идея крайне проста, и ее можно объяснить «на пальцах». Уже в самые ранние эпохи существования вселенной (первые доли секунды) плотность не распределена равномерно. Из-за флуктуаций (в инфляционной модели за эти вариации плотности ответственны квантовые эффекты) вещество распределено «где-то густо, а где-то пусто». Под действием гравитации области повышенной плотности могут сжиматься, а если масса и размер области соответствуют параметрам черной дыры, то и коллапсировать.

Существенно, однако, что вселенная еще очень молода. Поэтому сигналы (в том числе гравитационное взаимодействие) успели распространиться лишь на небольшое расстояние. Как говорят, «горизонт еще мал», т. е. размеры причинно-связанных областей невелики. Коллапсировать может лишь причинно-связанная область (иначе одна часть «не знает» о гравитационном влиянии другой). Если критическая комбинация массы и радиуса достигается лишь при большем размере, то придется подождать. По мере жизни вселенной размер горизонта растет как произведение времени на скорость света. Но не будем забывать, что и сама вселенная расширяется! Иначе говоря, области повышенной плотности могут растягиваться. И тут уж «кто кого переборет»: или размер горизонта успеет дорасти до нужного масштаба и произойдет коллапс, или флуктуация растянется и формирования черной дыры удастся избежать.

Важно, что коллапсирует область размером порядка текущего горизонта [109] Заметим, что существуют разные варианты механизмов формирования первичных черных дыр. В некоторых из них, например связанных с топологическими дефектами, история выглядит несколько иначе, и свойства черных дыр, в первую очередь их распределение по массам, будут иными. . Соответственно, в разное время формируются черные дыры разной массы: чем позже – тем больше [110] Вспомним, что «средняя плотность» черной дыры падает с ростом массы (а значит, и размера), так что какая-то относительно крупная область высокой постоянной плотности может соответствовать условиям коллапса в целом, а вот ее части схлопываться не будут. Таким образом, надо дождаться, когда космологический горизонт увеличится до соответствующего размера. . Процесс идет от самых ранних моментов (когда теоретически в некоторых моделях масса может доходить до планковской – 10 –5г) до примерно одной секунды (тогда могут образовываться дыры с массой около 100 000 масс Солнца). Для массы черной дыры в зависимости от времени формирования существует простая формула, определяемая массой вещества внутри горизонта:

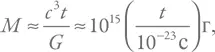
где c – скорость света, G – ньютоновская постоянная, а t – время.

Результат приведен в граммах, и время нормировано на момент формирования тех дыр, чья жизнь сейчас, согласно хокинговской модели, подходит к концу.

В своей знаменитой работе 1975 г. Стивен Хокинг предложил механизм, с помощью которого черная дыра может «испаряться» [111] Популярное изложение хокинговского испарения можно найти в книге Эмиля Ахмедова «О рождении и смерти черных дыр» (М.: МЦНМО, 2015). Также см. хорошее объяснение в заметке Игоря Иванова на сайте «Элементы» http://elementy.ru/novosti_nauki/432819/Nakonets_to_obnaruzhen_analog_izlucheniya_Khokinga_v_kholodnom_kvantovom_gaze . Важно заметить, что традиционное популярное описание этого процесса содержит неоправданные упрощения, а потому отчасти может запутать. Так что настоятельно рекомендую прочитать оба упомянутых в этой сноске источника. . Детали механизма довольно нетривиальны с бытовой точки зрения, а упрощенные иллюстрации лишь вводят в заблуждение. Но, как бы то ни было, вблизи горизонта (что не означает микроскопических расстояний от него!) за счет квантовых эффектов формируются частицы (и кванты электромагнитного излучения, и частицы, имеющие массу покоя), уносящие энергию дыры, т. е. уменьшающие ее массу. Чем меньше черная дыра, тем активнее она излучает. Для внешнего наблюдателя черная дыра выглядит как источник теплового излучения.

Температура излучения черной дыры определяется следующей формулой:

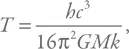
где h – постоянная Планка, а k – постоянная Больцмана.

Видно, что с уменьшением массы температура растет. Давайте попробуем получить эту формулу с точностью до численного коэффициента.

Начнем мы, как ни странно, с принципа неопределенности Гейзенберга и корпускулярно-волнового дуализма. Легенда гласит, что в разговоре с Яковом Борисовичем Зельдовичем Владимир Наумович Грибов высказал следующую мысль. Возникает парадокс, если мы применим принцип Гейзенберга к черным дырам. С одной стороны, мы говорим, что из них ничего не вылетает, а с другой – как же мы локализуем в маленькой черной дыре частицу, длина волны которой превосходит размер черной дыры? Иными словами, в некотором смысле квантовая механика вступает в противоречие с ОТО. Грибов полагал, что «квантовая механика победит».

Предельный масштаб, на котором мы можем локализовать частицу, связан с ее комптоновской длиной волны:

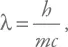
где m – масса частицы.

Что же это за длина волны? Это можно пояснить таким образом (хотя в таком упрощенном комментарии есть элемент передергивания). Каждой длине волны соответствует частота, которую можно рассчитать, используя скорость распространения волны. В данном случае – скорость света: ν = c /λ . С одной стороны, если мы рассматриваем волну, то энергия частицы будет равна E = hν . С другой – энергия частицы при такой предельной локализации будет порядка ее энергии покоя: E = mc 2 . Таким образом, hν = hc /λ = mc 2 . А отсюда мы сразу получаем, что

Принцип неопределенности Гейзенберга записывается таким образом: