Сергей Попов - Все формулы мира

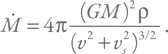
Если мы подставим в формулу типичные значения: ρ = 10 –24г / см 3, M = 2·10 34г, а для обеих скоростей возьмем значения 10 км/с (в случае скорости звука это типичное значение, а вот для скорости движения – скорее, нижний предел), то получим примерно 10 13грамм в секунду.

Теперь возникает более сложный момент – посчитать эффективность аккреции, т. е. сколько энергии выделится на грамм вещества, провалившегося в конце концов в черную дыру. И вот тут ясности нет. Дело в том, что поверхность-то у черной дыры отсутствует! Иначе говоря, выделить энергию при контакте с поверхностью невозможно. Значит, все энерговыделение должно идти в потоке. Насколько оно эффективно, в ряде случаев неясно. Если аккрецируемое вещество обладает достаточно большим орбитальным моментом, то вокруг черной дыры формируется аккреционный диск. За счет вязкости (по сути, за счет трения слоев газа друг о друга) энерговыделение достигает больших значений. Именно поэтому мы видим мощное излучение квазаров, блазаров и других активных галактических ядер, а также черных дыр в рентгеновских тесных двойных системах. В том случае, если и при аккреции из межзвездной среды формируется диск, можно рассчитывать на довольно значительную светимость. Давайте попробуем оценить верхний предел для нее.

Поступим очень просто. Оценим гравитационную потенциальную энергию на внутреннем крае аккреционного диска. В случае черных дыр существует важное понятие последней устойчивой круговой орбиты . Для невращающейся вокруг своей оси черной дыры (а мы думаем, что одиночные черные дыры, блуждающие по Галактике, в основном имеют относительно медленное вращение, поскольку раскрутить черную дыру можно в первую очередь мощной аккрецией в тесной двойной системе) радиус такой орбиты равен 6 GM / c 2, т. е. трем шварцшильдовским радиусам. После достижения этой границы вещество в диске очень быстро «вспираливается» под горизонт. Таким образом, плотность вещества в потоке под критическим радиусом мала, а потому там трудно сгенерировать мощное излучение за счет вязкости. На радиусе гравитационного захвата вещество имеет практически нулевую энергию. Значит, верхний предел на энерговыделение будет примерно равен по модулю потенциальной энергии на последней устойчивой орбите. Воспользовавшись приведенной несколько выше формулой для массы m , получим энерговыделение ( mc 2/ 6). Это много: каждый грамм будет давать 1,5·10 20эрг. Объединив это с полученной выше оценкой темпа аккреции и немного округлив, получим примерно треть светимости Солнца – довольно заметный источник!

Однако до сих пор одиночные аккрецирующие черные дыры не идентифицированы (здесь я нарочито избегаю слов «не обнаружены», поскольку потом может оказаться, что какие-то из известных слабых источников относятся к данному классу объектов). Расчеты показывают, что в спектре излучения одиночных аккрецирующих черных дыр может быть два максимума: в инфракрасной и рентгеновской области. Соответственно, предпринимались попытки выявить слабые источники с такими свойствами. Проводились специальные поиски в направлениях молекулярных облаков, где выше плотность среды, а значит, выше темп аккреции и, следовательно, светимость. Но все пока безрезультатно.

Вероятнее всего, приведенная выше оценка темпа аккреции завышает реальную величину, а значит, черные дыры будут более слабыми источниками. Однако нет никаких сомнений, что в Галактике блуждают многие десятки миллионов черных дыр звездных масс, потихоньку поглощающих вещество межзвездной среды. При этом выделяется какое-то количество энергии в виде электромагнитного излучения. Стало быть, рано или поздно они будут обнаружены.

А пока есть другой, уже работающий способ открывать одиночные черные дыры.

Любое тело обладает массой, а значит, искривляет пространство-время вокруг себя. Это сказывается на движении всех объектов в данной области. Разумеется, чем массивнее тело, тем на большем расстоянии оно может оказывать заметное влияние. Нас будет интересовать, как присутствие массивного тела сказывается на распространении электромагнитных волн, и в частности света.

Заметим, что отклонение световых лучей как таковое – это не совсем «изобретение» общей теории относительности. Согласно ньютоновской модели, свет, если представить его себе как поток очень легких частиц (именно так себе представлял свет сам Ньютон), также должен отклоняться, только эффект будет в два раза меньше, чем в ОТО [105] Здесь, правда, возникает противоречие с принципом Ферма. Я благодарен за это уточнение Эмилю Ахмедову. . Наблюдения смещения положения звезд во время солнечных затмений (а затем и другие многочисленные наблюдения и эксперименты) показали, что верен расчет в рамках ОТО – при небольших углах отклонения работает формула

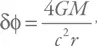
где δφ – угол, на который отклоняется свет, М – масса гравитационной линзы, а r – минимальное расстояние между траекторией светового луча и центром линзы.

Гравитационное линзирование встречается в астрономии в самых разных вариантах. В роли источника может выступать далекий квазар, а в роли гравитационной линзы – массивная галактика. Или же источником является далекая сверхновая, и ее свет линзируется на скоплении галактик. Мой любимый пример таков. Источником является аккреционный диск в далекой активной галактике, а его излучение линзируется на отдельных звездах более близкой галактики на луче зрения [106] Недавно добавился еще один поразительный пример. Мэнди Чен (Mandy Chen) и ее соавторы представили линзированное изображение галактики, на котором видно, что некоторые детали линзируются на сверхмассивной черной дыре в галактике-линзе. Это позволяет, в частности, определить массу черной дыры. Номер статьи в Архиве – 1805.05051. . В такой поразительной ситуации мы можем измерить параметры диска (по сути, определить, как его температура меняется с радиусом).

Однако здесь нас будет интересовать случай так называемого микролинзирования . Микро-, потому что линза относительно легкая, это объект звездной массы. Источником в такой ситуации обычно является звезда нашей Галактики, и, конечно, в ней же находится и линза.

Если мы смотрим на какую-то случайно выбранную звезду, то понадобятся сотни тысяч лет, пока еще какой-то умеренно массивный объект (другая звезда, бурый карлик или компактный остаток) пролетит столь близко к лучу зрения, что вызовет заметный эффект.