Карл Саган - Мозг Брока. О науке, космосе и человеке

SAGAN, C., “The Radiation Balance of Venus.” California Institute of Technology, Jet Propulsion Laboratory, Technical Report 32–34, 1960.

–, “The Planet Venus. “ Science , 133: 849 (1961).

–, The Cosmic Connection . New York, Doubleday, 1973.

–, “Erosion of the Rocks of Venus.” Nature , 261:31 (1976).

SAGAN, C., and PAGE T., eds., UFOs: A Scientific Debate. Ithaca, N. Y., Cornell University Press, 1973; New York, Norton, 1974.

SILL, G.,·”Sulfuric Acid in the Venus Clouds.” Communications Lunar Planet Lab., University of Arizona, 9: 191–198 (1972).

SPITZER, LYMAN, and BAADE, WALTER, “Stellar Populations and Collisions of Galaxies.” Ap. J ., 113: 413 (1951).

UREY, H. C., “Cometary Collisions and Geological Periods.” Nature , 242: 32–33 (1973).

–, The Planets , New Haven, Yale University Press, 1951.

VELIKOVSKY, I., Worlds in Collision . New York, Dell, 1965. (First printing, Doubleday, 1950.)

–, “Venus, a Youthful Planet.” Yale Scientific Magazine , 41: 8–11 (1967).

VITALIANO, DOROTHY B., Legends of the Earth: Their Geologic Origins . Bloomington, Indiana University Press, 1973.

WILDT, R., “Note on the Surface Temperature of Venus.” Ap. J ., 91: 266 (1940).

–, “On the Chemistry of the Atmosphere of Venus.” Ap. J ., 96: 312–314 (1942).

YOUNG, A. T., “Are the Clouds of Venus Sulfuric Acid?” Icarus , 18: 564–582 (1973).

YOUNG, L. D. G., and YOUNG, A. T., Comments on “The Composition of the Venus Cloud Tops in Light of Recent Spectroscopic Data.” Ap. J ., 179: L39 (1973).

Здесь мы рассматриваем вероятность того, что массивный объект такого типа, который имеет в виду Великовский, отделился от Юпитера и столкнулся с Землей. Великовский предполагает, что эта комета прошла по касательной рядом с Землей. Для простоты назовем эту идею столкновением. Рассмотрим сферический объект радиусом R , движущийся среди других объектов подобного размера. Столкновение произойдет, когда центры объектов окажутся на расстоянии 2 R . В таком случае мы можем говорить об эффективном поперечном сечении столкновения σ = π (2 R )2 = 4 πR 2; это площадь мишени, в которую должен удариться центр движущегося объекта, чтобы произошло столкновение. Давайте предположим, что только один такой объект (комета Великовского) движется, а остальные (планеты внутренней Солнечной системы) неподвижны. Это пренебрежение движением планет внутренней Солнечной системы может вызвать погрешность меньше, чем в два раза. Пусть комета будет двигаться со скоростью v , а пространственная плотность потенциальных мишеней (планет внутренней Солнечной системы) будет n . Мы будем использовать следующие единицы измерения: R – в сантиметрах (см), σ – в см2, v – в см/с и n – в количестве планет в 1 см3. Очевидно, что n – очень малое число.

Хотя у комет широкий диапазон углов наклонения орбит к плоскости эклиптики, ради гипотезы Великовского мы сделаем самое щедрое допущение, если примем самое малое возможное значение этого наклона. Если бы не было ограничений по наклонению орбиты кометы, она бы с одинаковой вероятностью двигалась бы повсюду в области пространства с Солнцем в центре и радиусом r = 5 астрономических единиц (1 а.е. = 1,5 × 1013 см), большой полуоси орбиты Юпитера. Чем больше пространство, в котором может перемещаться комета, тем меньше вероятность ее столкновения с другим объектом. Вследствие быстрого вращения Юпитера любой объект, вылетевший из него, будет двигаться в экваториальной плоскости планеты, угол наклона которой к плоскости вращения Земли вокруг Солнца составляет 1,2°. Однако, чтобы комета вообще достигла внутренней части Солнечной системы, ее отделение от планеты должно быть достаточно энергичным, так что возможно практически любое значение наклонения ее орбиты i . Самое низкое значение в таком случае – i = 1,2°. Следовательно, мы рассматриваем комету, которая движется (см. диаграмму) по орбите, проходящей где-то в клинообразном пространстве с центром в области Солнца (одним фокусом орбиты кометы должно быть Солнце) и с полууглом наклона, равным i . Ее объем тогда составляет: (4/3) πr 3 sin i = 4 × 1040 см3, то есть только 2 % от полного объема сферы радиусом r . Поскольку в этом пространстве находится (не считая астероидов) три или четыре планеты, пространственная плотность мишеней, относящихся к нашей проблеме, составляет около 10–40 планет/см3. Типичная относительная скорость кометы или другого объекта, движущегося по эксцентричной орбите во внутренней Солнечной системе, может составлять около 20 км/с. Радиус Земли R = 6,3 × 10 8 см, что почти точно равно радиусу планеты Венера.

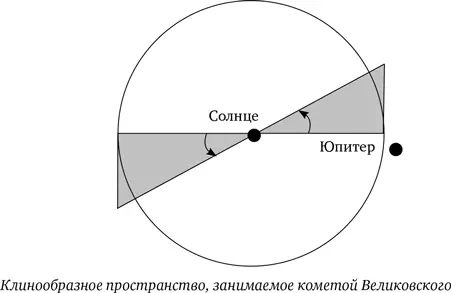
Сейчас давайте представим, что эллиптический путь кометы выпрямлен и что она движется какое-то время Т , пока не столкнется с планетой. В течение этого времени она проложит за собой воображаемый туннель объемом σ vT см³, и в этом пространстве должна поместиться только одна планета. Но 1/ n – также объем, вмещающий одну планету. Следовательно, две величины равны и справедливо равенство

T называется средним временем свободного пробега.

В реальности, конечно, комета будет двигаться по эллиптической орбите, и на время столкновения будут до какой-то степени влиять гравитационные силы. Тем не менее легко показать (см., например, Urey, 1951), что для типичных значений v и относительно кратких отклонений в истории Солнечной системы, какие рассматривает Великовский, гравитационное воздействие не должно сильно увеличить эффективное поперечное сечение σ, и грубое вычисление с использованием вышеприведенного уравнения должно дать приблизительно верные результаты.

У объектов, которые с давних времен в истории Солнечной системы оставляли ударные кратеры на Луне, Земле и внутренних планетах, сильно эксцентричные орбиты: это кометы и в особенности объекты группы Аполлона, которые являются или мертвыми кометами, или астероидами. Используя простые уравнения среднего времени свободного пробега, астрономы могут посчитать с хорошей точностью, скажем, количество кратеров на Луне, Меркурии или Марсе, образовавшихся за всю историю этих объектов: они образовались в результате случайного столкновения астероида из группы Аполлонов или реже какой-нибудь кометы с лунной или планетной поверхностью. Также уравнение точно прогнозирует возраст самых последних ударных кратеров на Земле, таких как Метеор, штат Аризона. Эти количественные соответствия между наблюдениями и физикой простого столкновения указывают на то, что и данную проблему можно рассмотреть в таком же ключе.

Теперь мы можем сделать вычисления применительно к основной гипотезе Великовского. В настоящее время нет аполлонов диаметром более нескольких десятков километров. Размеры объектов в астероидном поясе, и на самом деле везде, где столкновения определяют размеры, можно понять посредством физики измельчения. Количество объектов в данном диапазоне размеров пропорционально радиусу объекта в какой-то отрицательной степени, обычно от 2 до 4. Следовательно, если бы комета Великовского, превратившаяся в Венеру, была членом какого-то семейства объектов, как аполлоны или кометы, вероятность найти одну комету Великовского радиусом 6000 км была бы намного меньше одной миллионной вероятности найти комету радиусом 10 км. Более реалистичные оценки показывают, что эта разница вероятностей ближе к миллиарду, но давайте попробуем поверить Великовскому.