Карл Саган - Мозг Брока. О науке, космосе и человеке

Поскольку существует около десяти аполлонов радиусом более 10 км, вероятность, что среди них есть одна комета Великовского, в таком случае гораздо меньше 1 к 100 000. Равновесное содержание таких объектов составит тогда (для r = 4 а.е. и i = 1,2°): n = (10 × 10 –5) / 4 × 10 40= 2,5 × 10 –45комет Великовского на 1 см³. Среднее время свободного пробега до столкновения с Землей составит тогда: T = 1 / ( n σ v ) = 1 / [(2,5 × 10 –45 см -3) × (5 × 1018 см²) × (2 × 106 см/с -1)] = 4 × 10 21с ≃ 10 14лет, что гораздо больше возраста Солнечной системы (5 × 109 лет). Иными словами, если бы комета Великовского принадлежала к популяции других сталкивающихся обломков во внутренней Солнечной системе, она была бы таким редким объектом и, по сути, никогда не столкнулась бы с Землей.

Но давайте все же чисто теоретически допустим, что гипотеза Великовского верна, и зададимся вопросом, сколько потребуется его комете после отделения от Юпитера, чтобы столкнуться с планетой во внутренней Солнечной системе. В таком случае n обозначает распространенность планет-мишеней, а не комет Великовского, а T = 1 / [(10 –40 см -3) × (5 × 10 18см²) × (2 × 10 6 см/с -1)] = 10 15с = 3 × 10 7лет. Таким образом, вероятность того, что «комета» Великовского один раз столкнулась или прошла по касательной к Земле за последние несколько тысяч лет, равна (3× 10 4) / (3 × 10 7) = 10 –3, или 1 шанс из 1000, если она не принадлежала к другим популяциям обломков. Если же она принадлежала к таким популяциям, шансы поднимаются до (3× 10 4) / 10 14= 3 × 10 –10, или 1 шанс на 3 млрд.

Более точную формулировку теории орбитального столкновения можно найти в классическом труде Эрнста Эпика (1951). Он рассматривает мишень с массой m 0, с орбитальными элементами [214] Орбитальные элементы – набор параметров, задающих размеры и форму орбиты небесного тела, расположение орбиты в пространстве и место расположения небесного тела на орбите. – Прим. ред. a 0, e 0= i 0= 0, вращающуюся по орбите вокруг центрального объекта с массой M . Тогда у изучаемого объекта с массой m, с орбитальными элементами a, e, i и периодом P есть характерное время T до приближения на расстояние R к мишени, где

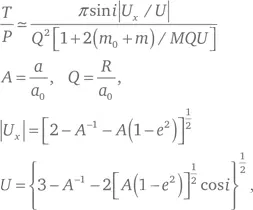
здесь: U – это относительная скорость «на бесконечности», а U x – ее компонент вдоль линии узлов (точек пересечения орбит).

Если R – физический радиус планеты, тогда

Для применения результатов Эпика к настоящей проблеме уравнения сводятся к следующему приближению:

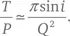
Используя P ≃ 5 лет ( a ≃ 3 а.е.), мы имеем:

или около ⅓ среднего времени свободного пробега из более простого аргумента выше.

Заметьте, что в обоих расчетах при приближении на N радиусов Земли вероятность физического столкновения возрастает в N ² раза. Таким образом, для N = 10, то есть прохождения на расстоянии 63 000 км, вышеприведенные значения T нужно снизить на два порядка. Это около 1/6 расстояния между Землей и Луной.

Для применения сценария Великовского необходимо более тесное сближение: в конце концов, книга называется «Столкновение миров» (Worlds in Collision). Также утверждается, что в результате прохождения Венеры мимо Земли вода в океанах поднялась до высоты 2,5 км. Исходя из этого, легко решить обратную задачу с помощью простой теории приливов (высота прилива пропорциональна M / r ², где M – это масса Венеры, а r – расстояние между планетами во время столкновения), что Великовский говорит о прохождении по касательной: поверхности Земли и Венеры соприкасаются! Но заметьте, что даже прохождение на расстоянии 63 000 км не освобождает гипотезу от проблем физики столкновения, которые очерчены в этом приложении.

И наконец, мы наблюдаем, что орбита, пересекающая орбиты Юпитера и Земли, подразумевает высокую вероятность близкого повторного подхода к Юпитеру, который выбросит объект из Солнечной системы еще до столкновения с Землей: естественный пример – траектория космического зонда «Пионер-10». Следовательно, нынешнее существование планеты Венера должно подразумевать, что комета Великовского сделала буквально несколько последовательных проходов мимо Юпитера и, следовательно, что ее орбита очень быстро стала круговой. (Великовский, должно быть, предполагает, что близкое прохождение кометы рядом с Землей произошло вскоре после ее отделения от Юпитера в соответствии с вышеприведенными вычислениями.)

В таком случае вероятность того, что комета столкнулась с Землей только через несколько десятков лет после ее отделения от Юпитера, составляет от одного шанса на 1 млн до одного шанса на 3 трлн, если допустить принадлежность обломков существующим популяциям. Даже если бы мы предположили, что комета отделилась от Юпитера так, как говорит Великовский, и сделали бы невероятное предположение, что она никак не связана с другими объектами, которые мы видим в Солнечной системе сегодня, то есть что малые объекты никогда не отделяются от Юпитера, среднее время, за которое она бы столкнулась с Землей, составляет около 30 млн лет, что не соответствует его гипотезе с шансом столкновения, равным одной миллионной. Даже если мы позволим его комете столетиями летать по внутренней Солнечной системе до приближения к Земле, статистика все равно не на стороне гипотезы Великовского. Когда мы учитываем тот факт, что Великовский верит в несколько статистически независимых столкновений за несколько сотен лет (читайте его книгу), общая вероятность того, что его гипотеза верна, становится совсем малой. Потребуются повторные столкновения планет, чтобы назвать их «столкновениями миров».

Гравитационное ускорение, которое держит нас на поверхности Земли, имеет значение 103 см/с² = 1 g . Замедление на a = 10 –2 g = 10 см/с² почти незаметно. Сколько времени τ потребовалось бы Земле, чтобы остановить свое вращение, если бы итоговое замедление было незаметным? Экваториальная угловая скорость Земли равна Ω = 2 π / P = 7,3 × 10 –5рад/с; экваториальная линейная скорость RΩ = 0,46 км/с. Таким образом, τ = RΩ / a = 4600 c, или немного больше часа.