Алим Войцеховский - ЗНАК ВОПРОСА 1997 № 04

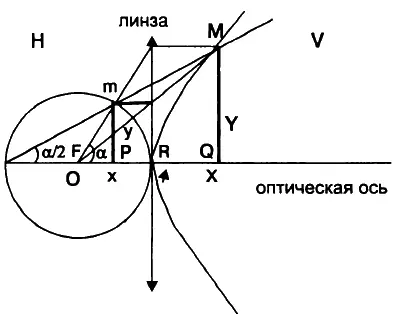
В модели Дьюрелла можно пользоваться поворотом на действительный угол а. Действительно, если точка m ( cos a. sin а ), принадлежит окружности, то точка M(l/cos a, tga) — гиперболе. Итак, гиперболе V-изображения будет соответствовать окружность в Н-проекции.　

Вычисления, основанные на использовании тригонометрических функций, позволили написать программу Durell. bas:

SCREEN 8

PI = 3.141593

COLOR 15, 1

M = 640: N = 200

LINE (.047 × M, 75 × N) — (.67 × M, 75 × N)

LINE (.414 × M, 10 × N) — (.42 × M, 0)

PRINT SPC(25); «у»; SPC(15); «Y»

PRINT

FOR k = TO PI / 3 STEP PI / 6

FOR i = 0 TO PI / 6 STEP PI / 150

t = 1 / 2 — (k + i)

x = (.234 +.19 × COS(t)) × M

у = (.75 —.3 × SIN(t)) × N

u = (234 +.19 / COS(t)) × M

v = (.075 — /3 × TAN(t)) × N

PSET (x, y)

PSET (u, v)

FOR w = 1 TO 1000

NEXT w

NEXT i

PRINT USING «it##.###»-, SPC(22); SIN(T);

PRINT USING «###.###»; SPC(9); TAN(t);

PRINT

LINE (.047 × M, 75 × N) — (u, v)

CIRCLE (x, y), 5

CIRCLE (u, v), 5

NEXT k

PRINT

END

Гиперболу можно рассматривать как изображение окружности в плоскости, где в качестве базиса берутся единичный вектор а, и мнимоединичный вектор b. «По существу, дело обстоит здесь совершенно так же, как и с картой земных полушарий, т. е. с изображением полусфер в виде плоских кругов. Это изображение неизбежно содержит искажения… Совершенно так же обстоит дело и в нашем случае, когда оригиналом является псевдоевклидова плоскость, а ее условным изображением — собственно евклидова плоскость чертежа», — пишет П. К. Рашевский в книге «Риманова геометрия и тензорный анализ».

В первой работе Эйнштейна (1905), в которой был сформулирован принцип относительности, еще не было языка неевклидовой геометрии. Это было сделано Минковским за несколько месяцев до смерти (наступившей в январе 1909 г.) в докладе, опубликованном посмертно. Его основной темой была геометрия, названная позже псевдоевклидовой геометрии, или геометрией Минковского, значение которой для теории относительности всегда подчеркивалось, Эйнштейном.

Формула линзы наглядно показывает относительность конечного и бесконечного . Романтики посвящали бесконечности и стихи. В начале романа «Отверженные» В. Гюго определил его как «драму, в которой главное действующее лицо бесконечность. Человек в ней — лицо второстепенное».

Повышенное внимание к «краевому мышлению» характерно не только для поэтов, но и для математиков. Математик Ж. Адамар в эссе «Исследование психологии процесса изображения в области математики», призывая «думать около», усматривает аналогии между краевым сознанием и расплывчатыми идеями, находящимися в «прихожей сознания» и время от времени выступающими на передний план, в поле ясного сознания. Вспомним историю отторжения векторного исчисления и неевклидовой геометрии. Очень показательно в этом отношении неприятие Вейерштрассом на его семинаре (в феврале 1870 г) системы неклассических геометрии Кэли-Клейна. «Я отнесся к этой отрицательной позиции с уважением и отложил в сторону уже созревшую идею. Я всегда робел перед критикой логиков, которая была далека от моих интересов. Только гораздо позже я понял, что суть дела заключается в различии наших подходов и что психология математического творчества таит в себе огромные проблемы. Очевидно, Вейерштрасс по натуре своей был склонен к тщательной, постепенной работе, шаг за шагом пролагающей путь к вершине; ему менее свойственно было издали распознавать не достигнутые еще высоты», — отмечал Ф. Клейн в «Лекциях о развитии математики в XIX столетии».

Система неевклидовых геометрий была впервые построена Феликсом Клейном, который опирался на алгебраическую работу Артура Кэли «On quantics». На прямой возникают три различные метрики: эллиптическая, гиперболическая и параболическая. Аналогично можно ввести метрику углов (в пучке прямых): эллиптическую, гиперболическую и параболическую, комбинируя все возможные типы мероопределения расстояния и углов, получаем 3 x 3 = 9 геометрий на плоскости:

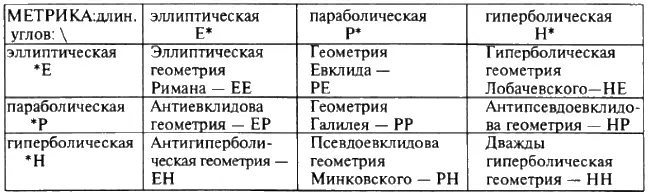
Геометрия Евклида, Галилея, Лобачевского и Минковского входят в систему Кэли-Клейна, что позволяет взглянуть на них с более общих позиций. Каждую геометрию можно охарактеризовать выражением для скалярного произведения векторов. В результате более чем столетней давности работ Кэли и Грассмана в геометрии открылся «королевский путь». Начиная с «Эрлангенской программы» Клейна, стало очевидным единство геометрии и алгебры. Действительно в математике мало понятий, которые было бы проще определить, чем понятие векторного пространства и преобразований в нем. Осознание того, что это установившийся процесс переосмысления , позволяет предположить, что «открытия, которые стоили стольких усилий…рискуют превратиться в дальнейшем в игрушки для школьников будущих поколений», — заключает Ж. Дьедонне, один из лидеров группы французских математиков, писавших под псевдонимом Н. Бурбаки.

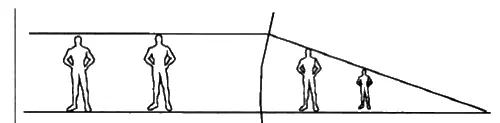
Дьюрелл моделирует лоренцево сокращение как оптическое сокращение. Действительно каждого, кто смотрел в бинокль на электричку, поражало, что ее вагоны выглядят смешными обрубками (которые чем дальше — тем короче). Место кажущегося схода параллельных рельсов (на горизонте) является с данной точки зрения бесконечно удаленной точкой. Расстояния между шпалами тоже укорачиваются в перспективе, которая формируется хрусталиком глаза (подобно линзе фотокамеры).

Процесс построения перспективного изображения состоит в том, что между глазом зрителя и объектом проводится луч, проходящий через прозрачную картинную плоскость , на которую проектируются точки предметной плоскости. Линия горизонта на картине находится на уровне глаз наблюдателя, На горизонте сходятся параллельные линии. Но они пересекаются между собой лишь в бесконечности.

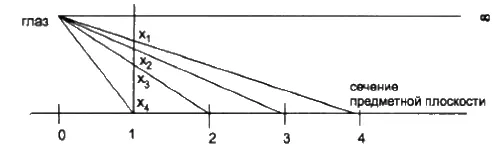
Это — удивительный факт и вместе с тем, первое, что узнает ученик художественной школы — это как изображать параллельные прямые!

Способ рисования изображен на известной гравюре Дюрера: