Александр Афанасьев - ЗНАК ВОПРОСА 1997 № 02

Дальнейшее обобщение понятия числа фактически означало увеличение размерности. Таковы были комплексные числа, имеющие действительную и мнимую часть. Введение мнимых чисел означало обобщение операции извлечения квадратного корня на случай, когда она невозможна. Оно связано с именем Дж. Кардано, который изобрел карданов вал, хорошо известный автомобилистам.

В школе учат, что квадратное уравнение х 2 = -1 не имеет решений, а в институте сообщают его решения х 1 = + i, х 2= — i в виде мнимых чисел. Вполне понятно, что введение мнимых чисел первоначально представляло несравнимо большие трудности, чем введение отрицательных чисел. Лейбниц называл их «чудом анализа, уродом из мира идей, двойственной сущностью, находящейся между бытием и небытием».

Именно парадоксальные объекты являются причиной поразительной эффективности математики. Введение отрицательных и мнимых чисел является ярким примером того, что парадокс не разрешается при помощи запретов и ограничений. При решении практических вопросов математики были вынуждены прибегать к помощи парадоксальных объектов, что означало переход от элементов к векторам.

Попытки свести массив к одному из его компонентов приводят к конфузу («Кто был ничем, так ничем и остался»). Например, попытайтесь ответить на вопрос: «Каково истинное поясное время на полюсе?» Там поясное время описывается набором векторов, учитывающим все направления. В двух диаметрально противоположных направлениях возможны две прямо противоположные ситуации:

Выделение аспектов единого объекта является обычным практическим решением в сложных логических ситуациях. Например, на Курском вокзале различают курское и горьковское направления.

Переход от отдельных элементов к массиву можно образно сравнить с переходом от майора к генерал-майору. Это качественный скачок в другую «октаву». Лучшим символом подобной ситуации является двуликий Янус. И это относится не только к богам. О Френсисе Дрейке, который был известным пиратом и адмиралом английского флота, говорят, что просто это был сложный человек в сложное время. Характерно, что фильм о разведчиках имел следующие названия серий: «Свой среди чужих» и «Чужой среди своих».

Сложная ситуация, описываемая парадоксом, может быть представлена парой противоположных векторов. В известном парадоксе Рассела полковой брадобрей должен брить только тех, кто не бреется сам. Тогда как же ему брить самого себя? Возможны две версии поведения брадобрея:

Двуликий любитель-профессионал подобен древнеримскому богу Янусу, который смотрит в разные стороны, но сердце у него одно.

Итак, брадобрей существует. Более того, существует «квадратный круг», используемый философами как синоним невозможного. Его даже проще представить себе, чем универсальную пробку («ко всем бочкам затычка»). Напомним, что три ее проекции стали эмблемой популярных (во всех смыслах) книг М. Гарднера по математике. Решение загадки дает эпюр Г. Монжа, окончившего Высшую политехническую школу и бывшего в России в составе наполеоновских войск. «Квадратный круг» — это вертикальный цилиндр. Действительно, его горизонтальной проекцией является круг, а вертикальной проекцией — квадрат.

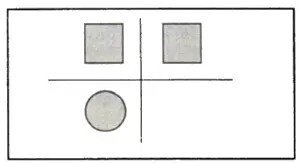
Слово «цилиндр» звучит непротиворечиво. Но парадоксально название эллиптического параболоида, форму которого имеет зеркало прожектора, создающего параллельный световой пучок. Именно его А. Толстой ошибочно назвал гиперболоидом (инженера Гарина). Кстати, мы указали фамилию писателя с именем, чтобы не путали с Л. Толстым. Впрочем, необходимо и отчество — А. Н. Толстой (а то есть опасность спутать с графом А. К. Толстым). Ф. И. О. — это трехмерный вектор (Ф, И, О).

Идея логической многомерности, выдвинутая автором под названием многоаспектностъ, является ключом к моделированию творческого мышления. Блеск возникает при рассмотрении в стереоскоп пары из черного и белого. Каждый может сам проделать маленький опыт. Слегка скосив глаза, совместите внутренний черный квадрат с белым и тогда… он заблестит и ПОДНИМЕТСЯ. восстав «крышей» усеченной пирамиды.

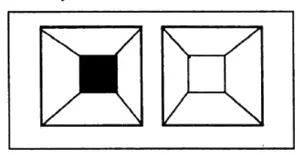
Чудо — это просто!

Многие читатели, видимо, уже получали удовольствие от рассматривания стереограмм в книгах популярной сейчас серии книг «Волшебный глаз. Третье измерение», издаваемых в ФРГ.

Парадоксы возникают, когда пытаются отделаться односложным ответом на сложный вопрос. Все новое воспринимается как «бред» (парадокс), а потом как «очевидность» (разрешение парадокса). Так, первоначальное неприятие неевклидовой геометрии объяснялось тем, что парадоксальные результаты не укладывались в одномерную логику — блеск ума непостижим для автора плоских шуток (подобно тому как одноглазому не объяснить, что пара из черного и белого дает стереоэффект блеска). Чернышевский из сибирской ссылки писал сыну: «Перестань заниматься неевклидовой геометрией! Математики я не знаю, но знаю достаточно, чтобы утверждать, что это — ерунда». Признанный король математиков Гаусс не опубликовал свои труды по неевклидовой геометрии, ибо, по собственному признанию, «боялся криков беотийцев» (синоним самых тупых в Древней Греции). Эта участь постигла Лобачевского. Об этом можно прочесть в книге А. Ливановой «Три судьбы» (М.: Знание, 1969). Только 26 лет спустя, перечитывая ее как бы заново, я прочувствовал, каким смелым может быть анонимный рецензент, издеваясь даже над названием: «его Геометрия отлична от употребительной, которой мы все учились… и есть только воображаемая. Да, теперь всё очень понятно. Чего не может представить воображение особливо живое и вместе уродливое ? Почему не вообразить, например, черное белым, круглое четырехугольным, сумму всех углов в прямолинейном треугольнике меньше двух прямых? Очень, очень можно, хотя для разума все это и непонятно» (курсив мой. — К.Б.). Блеск ума оказался непостижим для рецензента, и ответа Лобачевского редакция не напечатала. Впрочем, до нас дошел его сдержанный, полный достоинства ответ, опубликованный его родным университетом вместе с текстом мемуаров «Воображаемая геометрия»: «Рецензент основал свой отзыв на том только, что моей Теории не понял и почитает ее ошибочной…» Через 7 лет (в 1842 г.) Лобачевский был избран членом-корреспондентом Геттингенского ученого общества по представлению Гаусса.