Александр Афанасьев - ЗНАК ВОПРОСА 1997 № 02

2. «Ни один х не есть z» — общеотрицательное суждение.

3. «Некоторые х суть z» — частноутвердительное суждение.

4. «Некоторые х не есть z» — частноотрицательное суждение.

Например, суждение «Все ученые смертны» является общеутвердительным, а суждение «Некоторые ученые смертны» является частноутвердительным. При арифметизации будем кодировать утверждение числом +1, отрицание числом —1. В дальнейшем часто будем просто ставить «+» и «—". Отсутствие информации будем обозначать числом 0.

Частноутвердительному суждению соответствует положительный вектор, а общеотрицательному суждению — отрицательный вектор. Если обозначить: мученые, у = люди, z = смертные, то вектор (+ 0 +) будет обозначать частноутвердительное суждение «Некоторые ученые смертны» = «Некоторые х суть z», а вектор — (+ 0 —) — общеотрицательное суждение «Ни один ученый не бессмертен» = «Ни один х не есть не — z». Эти два вектора дают общеутвердительное суждение «Все ученые смертны» = «Все х суть z».

Получение логического заключения сводится к исключению термина-посредника «у» (среднего термина силлогизма). Приведем пример силлогизма, который состоит из общеутвердительных суждений:

«Все люди смертны»

«Все ученые — люди»

«Все ученые смертны»

В векторных обозначениях приведенный выше силлогизм может быть записан в следующем виде:

При решении проблемы разрешимости силлогизмов решающую роль играет принцип аннигиляции. Заключение следует из данных посылок при условии ровно одной аннигиляции при сложении или вычитании векторов.

В заключение получаем положительный вектор как разность (1,1,0) — (0,1, —1)= = (1,0,1), а отрицательный вектор — как знак суммы отрицательных частей (0,1, —1) + (1, _1,0) = (1,0, —1). Заключение принимается, когда сумма отрицательных частей или хотя бы одна перекрестная разность дает ровно один нуль.

Другая разность (0,1,1) — (1, -1,0) = (-1,2,1) отвергается (ибо число 2 в заключение указывает на несовместность утверждения +1 и отрицания —1).

Приведем текст программы Aristotle.bas для решения силлогизмов:

PRINT

SCREEN 8: COLOR 7, 1: DIM х(4, 2, 3)

PRINT " ЕСТЬ х у z НЕТ х у z": PRINT

FOR k = 1 ТО 2

FOR i = 1 ТО 2

PRINT SPC(6);

FOR j = 1 TO 3

READ x(k, i, j)

PRINT x(k, i, j);

NEXT j

NEXT i

PRINT

NEXT k

PRINT "………………………."

FOR j = 1 TO 3

x(3, 2, j) = SGN(x(1, 2, j) + x(2, 2, j))

x(3, 1, j) = x(1, 1, j) — x(2, 2, j)

x(4, 1, j) = x(2, 1, j) — x(l, 2, j)

NEXT j

PRINT SPC(6); x(3, 1, 1); x(3, 1, 2); x(3, 1, 3);

PRINT SPC(6); x(3, 2, 1); x(3, 2, 2); x(3, 2, 3)

PRINT SPC(6); x(4, 1, 1); x(4, 1, 2); х(4, 1, 3)

DATA 1,1,0, 1, -1,0

DATA 0,1,1, 0,1, -1

END

Автором написана программа Carroll.bas, позволяющая получать также чертеж диаграммы Кэрролла.

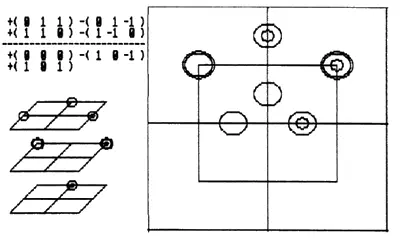
На диаграмме верхняя и нижняя половины соответствуют +х и — х, левая и правая половины соответствуют +z и — z ,внутренний квадрат и его внешность соответствуют +у и — у:

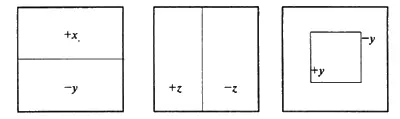
Всевозможные комбинации х, у и z приводят к различным тройкам (х, у, z).

Фактически, это — трехмерная диаграмма. Поэтому для сравнения слева приведено ее представление в виде куба.

Для освоения диаграмм Кэрролла была написана простая программа-тренажер С 2, которая позволяет для трехбуквенной диаграммы Кэрролла (приведенной в заставке) освоить расположение ячеек, задаваемое трехмерными векторами (х, у, ) В отличие от Аристотеля, у Кэрролла выводим силлогизм:

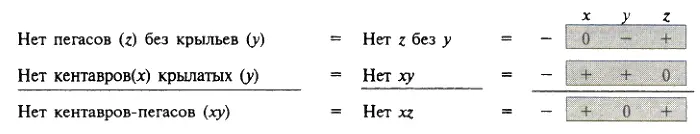
По 1-му правилу Кэрролла: из двух Химер с исключаемыми терминами различных знаков следует Химера, в которой оставляемые термины сохраняют свои знаки. За счет включения негативной силлогистики выводимы 624 модуса.

Рассмотрим еще один интересный пример из книги Л. Кэрролла. Если обозначить х = уроки, у = трудные, г = требующие особого внимания, то пример № 22 может быть записан в виде:

Некоторые уроки трудны = Некоторые х суть у

То, что трудно, требует особого внимания = Все у суть

Некоторые уроки требуют особого внимания» = Нек. х суть z

Заключение получаем как разность (1, 1, 0) — (0, 1, -1) = (1, 0, 1).

Приведем также решение многопосылочного силлогизма:

Ни одна утка (х) не танцует вальс (и)

Ни один офицер (z) не откажется танцевать вальс (и)

Все мои домашние птицы (у) — утки (х)

Все мои домашние птицы (у) — не офицеры (-z)

Предложенный алгоритм сводит выполнение умозаключений к действиям с компонентами логических векторов (записанных в троичной системе счисления). Многоаспектный метод является аналитическим методом, который применим для логических векторов любой размерности. Будет поучительно рассмотреть полисиллогизм из книги Кэрролла:

1. Ни один из встреченных в море, но оставшихся незамеченными предметов — не русалки.

2. Предметы, занесенные в вахтенный журнал, стоят того, чтобы их запомнить.

3. В моих путешествиях я не видел ничего такого, что стоило бы запомнить.

4. О встреченных в море и замеченных предметах делается запись в вахтенном журнале.

Запишем его через пятимерные векторы: (x1, х2, хз, х4, x5) = х, у, z, и, v).

Заключение: «Я никогда не видел ни одной русалки». С помощью диаграмм Кэрролла решение этого полисиллогизма получить нельзя, ибо увеличение размерности выше четырех делает геометрический метод непригодным. Традиционные способы решения применимы только к силлогизмам с тремя терминами. Они основаны на классификации модусов на 4 фигуры и требуют запоминания мнемонических латинских слов.

«Сперва хочу вам в долг вменить

На курсы логики ходить…

В мозгах, как на мануфактуре,

Есть ниточки и узелки.

Посылки не по той фигуре

Грозят запутать челноки».

Лучше затратить труд на освоение аналитического метода, чтобы потом легко получать решения любых силлогизмов. Поразительная эффективность диаграмм Кэрролла по сравнению с кругами Эйлера основывается на использовании помимо положительных и отрицательных ячеек еще пустых ячеек. Это — ситуация неопределенности, отсутствия информации, которая обозначается нулем и возникает при аннигиляции. Действительно, знать, что фишка находится в левой или в правой половине — это значит ничего не знать о ее местонахождении.