Олег Власов - Футболоматика: как благодаря математике «Барселона» выигрывает, Роналду забивает, а букмекеры зарабатывают состояния

Скоординированное движение является ключом к успешной защите. Сначала четверка защиты одновременно делает шаг вперед, и это важно для всей команды в целом. Равномерно распределяясь по всему полю, обороняющаяся команда создает сеть, которая препятствует дальнейшему продвижению. Частично такая согласованность достигается путем следования за мячом, но она также зависит и от игроков: они должны следить за перемещениями друг друга, чтобы сеть оставалась прочной.

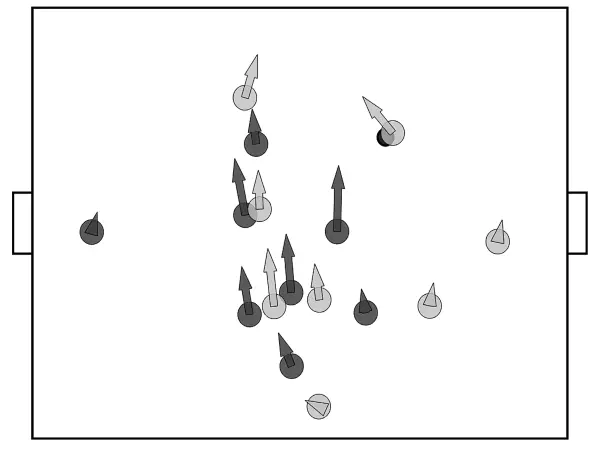
Рисунок 9.3. Позиции и направления игроков во время тренировочного матча резервной команды «Нюрнберга». Снимок сделан примерно через секунду после рисунка 9.1.

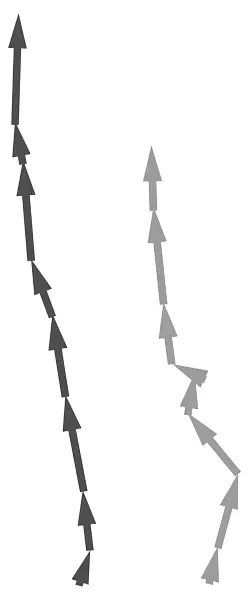
Рисунок 9.4. Измерение координирования игроков в обеих командах путем соединения их стрелок, указывающих направление.

На первый взгляд может показаться, что для поддержания прочной защитной сети игроки должны отслеживать всех своих товарищей по команде. Однако еще в 1995 году Тамаш Вищек и его коллеги разработали модель, которая доказывала, что выравнивание группы может быть достигнуто и без следования за мячом, и даже с очень ограниченным знанием позиций и направлений остальной части команды [97] Vicsek, T. Novel type of phase transition in a system of self-driven particles. – Physical Review Letters 75(6), 1995. – p. 1226–1229. . Представьте, что вы бежите по полю размером 100 на 100 м (почти в два раза больше футбольного поля) с 43 другими людьми (ровно вдвое больше стандартного количества игроков в футбольном матче). Вы бежите со скоростью 12 км/ч – достаточно быстрой трусцой. Это поле имеет странное свойство: если вы сбегаете с одной стороны, то вы возвращаетесь на другую. Поэтому, если вы сбегаете с верха, вы снова появляетесь внизу, и если вы забегаете слишком далеко влево, вы снова оказываетесь справа. Конечно, в действительности такого поля не существует, но здесь вы представляете себя внутри математической модели. Поэтому странные предположения сейчас допустимы.

Согласно модели Тамаша вы должны посмотреть на своих ближайших соседей – допустим, тех, кто находится в пределах десяти метров от вашей текущей позиции, – и начать двигаться в том же направлении, что и они. Представим себе, что все остальные 43 игрока, застрявшие в этом поле, делают то же самое, и посмотрим, что произойдет. На рисунке 9.5 показана симуляция позиций и направления движения всех 44 людей (включая вас) спустя 1 секунду, 20 секунд и 2 минуты бега.

В начале (рисунок слева) все движутся в случайном направлении. Серый круг в центре показывает ваше местоположение и позиции ваших соседей в радиусе десяти метров. Вы начинаете двигаться в направлении вашего ближайшего соседа. Через 20 секунд, в середине рисунка, уже образовались небольшие группы. Вы находитесь в одной из групп, направляющихся вверх влево, но другие группы движутся в разных направлениях. Через две минуты, как показано справа на рисунке, вы уже сделали пару кругов по полю. Поскольку вы бегаете по кругу, вы все еще следуете за несколькими соседями, но теперь все поле движется примерно в том же направлении, что и вы.

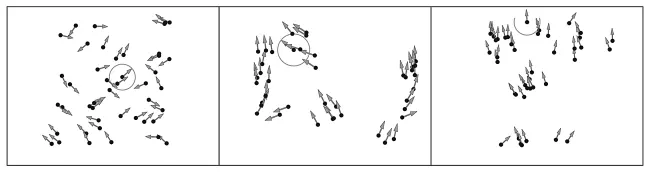
Рисунок 9.5. Позиция и направление 44 моделируемых людей, которые бегают по полю с краями телепортации. Результаты моделирования через 1 секунду (слева), 20 секунд (посередине) и 2 минуты (справа). Серые круги указывает на вашу позицию и на людей, за которыми вы следуете.

Чтобы выйти на единый курс, людям в нашей симуляции требуется меньше двух минут, и даже спустя 20 секунд большинство из них двигаются в одном направлении. Вы согласовываете свои действия с остальными без лидера, без разговоров или любого вида общения и без предварительного плана. Все, что вам нужно делать, – это бегать кругами примерно в том же направлении, что и вашим ближайшим соседям, и группа скоординируется.

Вы можете провести этот эксперимент самостоятельно. Просто найдите несколько людей и открытую площадку и скажите им двигаться в том же направлении, что и соседи. Поскольку у вас, вероятно, нет телепортера, вам придется сказать им оставаться на поле. Но результат будет подобным: очень скоро вы получите круговое движение по часовой или против часовой стрелки. Все будут двигаться друг за другом вокруг открытого пространства [98] Dyer, J. R. G. Leadership, consensus decision making and collective behaviour in humans. – Philosophical Transactions of the Royal Society B: Biological Sciences 364(1518), 2009. – p. 781–789. .

В модели Тамаша телепортация с одной стороны поля на другую означает отсутствие ограничений в направлении движения. Это создает ощущение пребывания посреди гигантской стаи скворцов или роя саранчи. Например, стая скворцов в сумерках может состоять из нескольких тысяч птиц, но каждый из них реагирует только на несколько ближайших соседей. Точно так же летающий рой саранчи может покрыть десятки или даже сотни квадратных километров, но отдельные особи взаимодействуют в первую очередь с теми, что находятся всего в нескольких сантиметрах. Модель Тамаша помогает объяснить, как эти стаи могут формироваться без внешнего сигнала, который бы указывал саранче направление движения. Саранче не нужно следить за ветром или солнцем – локальных взаимодействий достаточно для того, чтобы заставить их двигаться в одном направлении.

Модель Тамаша была тщательно проверена на саранче, рыбе, птицах и других животных [99] Я был частью команды, которая провела один из первых таких тестов. Подробности – в статье: Buhl, J. From disorder to order in marching locusts. – Science 312(5778), 2006. – p. 1402–1406. . Детали взаимодействия видов различны, но принципы одинаковы. Локальные взаимодействия между соседними особями позволяют группе в целом координировать свои действия. Это хорошая новость для футболистов. Если насекомые с не самым большим мозгом могут перемещаться вместе в больших группах на огромные расстояния в течение нескольких месяцев, то не должно составить труда заставить 11 игроков двигаться в унисон вперед-назад по футбольному полю в течение 90 минут. Модель Тамаша подразумевает, что игрокам не нужно отслеживать позиции и направления всех своих товарищей по команде и представителей соперника для координации. Им просто нужно следить за соседями. Общая координация будет выполняться автоматически.

В исследовании команды из португальской Примейры Угу Фольгаду с коллегами обнаружил, что для разных позиций синхронизация варьируется [100] Folgado, H. Competing with lower level opponents decreases intrateam movement synchronization and time-motion demands during pre-season soccer matches. – PLoS One: e97145, 2014. . Защитники и центральные полузащитники показывают лучшее взаимодействие. Они движутся вместе, либо опекая соперника (если мяч находится на другой половине поля), либо активно прессингуя (если мяч уже на их половине). У нападающих наиболее низкий уровень координации, поскольку они пытаются запутать игроков оппозиции непредсказуемыми рывками и забегами. Это похоже на тот рисунок, который мы видели в тренировочной игре «Нюрнберга», где защищающаяся команда была более выстроенной.