Александр Селюцкий - Вдохновение по заказу. Уроки изобретательства

Мы заменяем термины словом «штуковина», оно играет у нас ту же роль, какую играет в математике «икс». Поначалу инженеры посмеивались, заменяя «штуковипой» привычные термины «вибродатчик», «экстрактор», «опалубка», «коррелометр». Но довольно скоро обнаружилось, что любую задачу можно изложить без терминов.

Психологическая инерция отступает, но не сдается. Уже нет слов, навязывающих старые, привычные представления, но остается старый зрительный образ. Я не произношу слово «ледокол», но все равно у меня перед глазами нечто ледоколообразное.

Чтобы преодолеть психологическую инерцию, мы используем оператор РВС. Это шесть мысленных экспериментов, которые последовательно расшатывают привычное зрительное представление. Мысленно увеличиваем размеры (или другой основной параметр) «штуковины» в тысячу, в миллион раз... уменьшаем размеры... увеличиваем продолжительность процесса... уменьшаем... увеличиваем допустимую стоимость... уменьшаем...

Оператор РВС не всегда дает решение задачи. Собственно, он п не предназначен для этого. Его цель — сбить психологическую инерцию перед решением. Но задача о водоводе несложная, и в листках с выполненным домашним заданием я сразу замечаю много правильных ответов.

Что ж, возьмем наугад одну работу (странный феномен: наугад я почему-то всегда вытаскиваю работы, написанные хорошим почерком).

«1. Р-^оо. Размеры бетонной штуковины увеличиваются в сто раз. Громадина наподобие Останкинской башни. Никакие краны не годятся, это ясно. Как уложить махину высотой в четыре километра и диаметром в километр? Нет, это не башня, у башни диаметр мал сравнительно с высотой. Это гора. Как уложить гору? Идеально было бы, если бы гора легла сама. Но горы никогда не падают. Не знаю. Задача стала сложнее. Этот шаг ничего не дал.

2. Р—Ю. Для начала уменьшим размеры в сто раз. Высота 40 см. Все очень просто: уложим штуковину вручную. Высота 0,4 см. Снова вручную. Высота 0,04 мм. Задача опять усложнилась.

3. В >-оо. В условиях задачи не указано, сколько времени отводится на спуск штуковины. Предположим, месяц. Увеличим этот срок в 100 раз. 8 лет. Не вижу особой разницы. Увеличим срок еще в 1000 раз. 8000 лет. Осядет грунт и штуковина опустится сама? Во всяком случае, за 8 миллионов лет могут произойти большие геологические изменения.

4. В—М3. Штуковина опустилась за одну минуту или за одну секупду. Это значит, что она упала. Чтобы штуковина упала, ее центр тяжести должен изменить свое положение.

Появилась идея, относящаяся к пункту 1. Есть горы, которые сами падают. Это — айсберги. Подтаивает основание, смещается центр тяжести, гора опрокидывается. Пункт 3 тоже наводит на подобную мысль: за миллионы лет могут выветриться, вымыться самые твердые породы. Отсюда идея...»

Далее идет описание. Все верно, можно ставить пятерку, решение совпадает с изобретением по авторскому свидетельству № 194294, в котором сказано: «Способ монтажа тяжелых конструкций путем опускания их на рабочее место, отличающийся тем, что с целью упрощения процесса монтажа под конструкцией возводят колонны из природных веществ — льда, соли, которые затем у основания соответственно растапливают и растворяют, обеспечивая тем самым уменьшение длины колонн с одновременным опусканием конструкции».

Другая работа.

«1. Р—>-оо. Начнем с увеличения в миллиард раз. Получается, что длина штуковины 40 миллионов километров. Диаметр Земли — 12 тысяч километров. Положить такую штуковину на Землю нельзя. Можно Землю положить на нее. Новая формулировка задачи: как откос положить на водовод? На откосе должно что-то нарасти. Нужно иметь что-то (например, подушку со сжатым воздухом), способное увеличиваться и уменьшаться. Когда водовод изготовлен, пространство между откосом и водоводом должны заполнить маленькие человечки. Те человечки, которые окажутся около водовода, прочно вцепятся в его поверхность. А потом толпа человечков начнет редеть (испарение, таяние?). Водовод наклонится (его потянут человечки) и постепенно ляжет на откос.

Решение: заполнить пространство между откосом и водоводом льдом, приморозить трубу ко льду и постепенно расплавлять лед, чтобы он уходил из этого пространства. Вместо льда можно взять какое-нибудь химическое вещество п действовать на него реактивом, но лед дешевле».

Придется усложнить задачу, слишком легко с ней справляются. В этом решении есть любопытный нюанс: лед положен не под тРУбу» а рядом с ней, в пространстве между трубой и откосом. Использована способность льда хорошо сцепляться с бетоном, это остроумно. Следовало бы поставить пятерку. Но отработан только один шаг оператора РВС, в другой раз это может подвестп: опасно останавливаться на первой подходящей идее. И потом, меня смущают маленькие человечки: хорошо пли плохо, что они применены здесь? Все-таки это упражнение на оператор РВС.

Преодолев психологическую инерцпю, я ставлю оценку

5 ±0,5.

эпизод пятый

ПОДОЗРИТЕЛЬНО ПРОСТАЯ ЗАДАЧА

Задача. На стальном тросе А висит груз. В плоскости, перпендикулярной тросу А, движется трос Б. Как сделать, чтобы трос Б, продолжая движение, не разорвал бы трос А и сам не был бы разорван?

Я оставляю магнитофон и выхожу в коридор. Пусть решают самостоятельно. Устраиваюсь у окна, закуриваю. Докурить мне не удается, зовут в класс.

— Повторите, пожалуйста, условия.

Повторяю.

— И это все?

— Все.

— Тогда задача решена. Мы думали, там есть еще что-то. Подозрительно простая задача.

Включаю магнитофон.

«— Веселая ситуация. Можно показывать в цирке: трос проходит сквозь трос, а тому хоть бы что... На грани фантастики.

— Раз ситуация фантастическая, позовем золотую рыбку. Трос А может свободно дойти до троса Б. Это реальность Р\. А вот остальное — фантастика.

— Почему? Трос А может частично войти в трос Б. У троса Б должен быть какой-то запас прочности, обрыв произойдет не сразу.

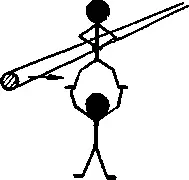
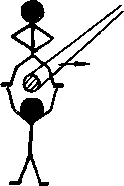
— Значит, мы разложили Ф\ на Р2 п Ф2.

— <���Х>2 тоже можно разложить. Трос А может полностью пройти сквозь трос Б, это реальность Рз. А вот совпадение оборванных концов — это уже фантастика, то есть Фз.