Рудольф Ташнер - Число, пришедшее с холода. Когда математика становится приключением

в точности соответствует старому школьному правилу: для того чтобы возвести в степень число, выраженное степенью, надо перемножить показатели степени.

Самое большое число, которое можно записать всего тремя цифрами, выглядит так:

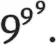
Это степенная башня, состоящая из трех девяток. Это число начинается с 4281… и содержит 369 693 100 разрядов.

Профессор информатики Стэнфордского университета Дональд Кнут заменил придуманный Брадвардином способ записи степеней новой символикой, которая лучше подходит для программирования, выполняемого обычным текстом. Например, степень 3² Кнут предложил записывать так: 3↑2. Вертикальная стрелка словно заменяет команду считать следующее число показателем степени. Таким же способом, как открыл Кнут, можно сокращенно записывать и степенные башни. Например, символами 3↑↑2 записывают степенную башню, состоящую из двух чисел 3. Это означает 3↑↑2 = 3↑3 = 3³ = 27. Здесь пока не заметно ничего особенного, но хитрость таится в самой записи двух вертикальных стрелок! Ибо 3↑↑3 — это уже степенная башня, состоящая из трех троек, то есть

3↑↑3 = 3↑3↑3 = 3 3³ = 3 27 = 7 625 597 484 987,

а 3↑↑4 — это степенная башня, состоящая из четырех троек, то есть

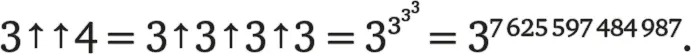
Этот числовой великан начинается с 1258… и содержит 3 638 334 640 025 разрядов, то есть он больше числа, записанного в виде степенной башни из трех девяток, которая с помощью метода Кнута записывается так: 9↑↑3.

Мало того, Кнут расширил свое обозначение еще на один шаг. Если он помещал между двумя числами три вертикальные стрелки, то число, стоящее справа от тройной стрелки, говорило, сколько раз надо было записать число, стоящее слева, и поставить между ними двойные стрелки. В этом случае с записью Кнута работают, как со степенной башней — то есть справа налево. Например, запись 3↑↑↑2 есть сокращенная запись 3↑↑3. Это число мы с грехом пополам еще можем себе представить — 7 625 597 484 987. Но, например,

3↑↑↑3 = 3↑↑3↑↑3 = 3↑↑7625597484987.

Здесь речь идет о степенной башне, в которой над основанием 3 надо написать косо друг над другом 7 625 597 484 986 троек. Работать с такой степенью надо начинать с ее верхнего шпиля.

Число 3↑↑↑3 так велико, что нет ни малейшего шанса даже приблизительно определить число его разрядов, и невозможно сказать, с каких цифр оно начинается [10].

Число, вынесенное в подзаголовок, несколько больше четырех с четвертью миллиардов. Даже находясь под впечатлением числовых монстров Кнута, мы понимаем, что это довольно значительное число. Особенно сильно оно впечатляет, если представить его в виде денежных купюр. В мире не так уж много людей, чье личное состояние превосходит четыре миллиарда евро. Напротив, министры финансов ежедневно оперируют подобными суммами. При этом они чаще говорят о «приблизительно 4,3 миллиарда», щедро, с избытком, округляя эту величину на какие-то жалкие пять миллионов. Правда, чиновники Министерства финансов являются, не в пример своим начальникам, куда более педантичными. В 1920-х гг.

4,3 миллиарда марок, наоборот, считались смехотворно малой суммой. В ноябре 1923 г. в Германии на 10 миллиардов марок можно было купить разве что почтовую марку. Купюрами достоинством в миллионы марок в ту холодную осень буквально растапливали печки. 297 марок в конце приведенной выше суммы не стоил, наверное, даже во́лос. 16 ноября 1923 г. за сумму, в тысячу раз большую, чем 4,2 миллиарда марок, то есть за 4,2 триллиона марок, можно было купить целый доллар.

Представим себе расстояние 4 294 967 297 метров. Это очень большое расстояние, оно в сто раз превышает окружность Земли по экватору. Служащие авиакомпаний, часто летающие на самолетах деловые люди, да и многие простые смертные давно преодолели это расстояние. Луна находится от Земли на расстоянии, составляющем менее одной десятой этого отрезка.

Напротив, размер атома измеряют в ангстремах, единицах, составляющих одну стомиллионную долю сантиметра. Если взять 4 294 967 297 атомов размером 1 ангстрем и расположить их в ряд, то мы получим цепь длиной менее полуметра.

4 294 967 297 секунд. Звучит устрашающе. Но тем не менее назвать этот период времени чрезвычайно долгим нельзя. Всего это составит 136 лет и немного больше 37 дней, то есть время смены четырех поколений.

Отрезок времени 4 294 967 297 лет по длительности превышает предыдущий период более чем в тридцать миллионов раз. Это действительно период времени гигантской продолжительности. Четыре миллиарда лет назад только что затвердела кора Земли и возник Мировой океан. Вся наша Вселенная существует всего в три раза дольше.

4 294 967 297 тонн представляются невероятным, просто исполинским весом, и это в самом деле так, но в сравнении с массой Земли, превосходящей данную массу более чем в триллион раз, названный вес можно считать пренебрежимо малым.

Представим себе гордого обладателя 4 294 967 297 атомов золота и прикинем, сколько у него этого благородного металла. Окажется, что лишь смехотворных 0,000 000 000 0014 грамма. Такое количество невозможно взвесить на лабораторных весах, настолько оно мало.

Таким образом, число 4 294 967 297 можно считать большим или маленьким в зависимости от того, в каких единицах это число измеряют.

Но что, если мы не станем связывать это число ни с какими единицами, если отвлечемся от экономики, космического пространства, времени, материи, если мы посмотрим на число 4 294 967 297 просто как на число, и ни на что больше? Не откроем ли мы в нем что-нибудь особенное? Если отвлечься от приближенного значения 4,3 миллиарда, то мы сразу убедимся в том, что это число нечетное, то есть оно не делится на два. Тот, кто еще немного помнит школьный курс математики, знает, как установить, делится ли какое-либо число на три. Число делится на три, если сумма его цифр делится на три [11]. Сумма цифр числа 4 294 967 297 равна

4 + 2 + 9 + 4 + 9 + 6 + 7 + 2 + 9 + 7 = 59.

59 не делится на три, а это значит, что число 4 294 967 297 не делится на три. Поскольку число это не имеет в разряде единиц ни нуля, ни пятерки, оно также не делится на пять.

Может быть, 4 294 967 297 является простым числом?

Числа, отличные от единицы, которые нельзя представить в виде произведения, то есть не являющиеся истинно прямоугольными числами, называют простыми. В отличие от простых так называемые «составные» числа являются числами истинно прямоугольными. Это означает, что такие числа можно представить в виде произведения двух чисел, из которых оба больше единицы. Геометрическая иллюстрация: можно изобразить прямоугольную решетку, число точек которой в точности равно составному числу. Действительно, если умножить число точек в строке на число точек в столбце, то получится все составное число целиком. Поскольку Пифагор и его ученики — заметим, кстати, что среди них были и женщины — имели пристрастие изображать числа в виде рисунков из точек, постольку понятие простого числа, вероятно, возникло в то же время, когда была изобретена математика, то есть в VI в. до н. э.