Коллектив авторов - На плечах гигантов

Но, по подобию треугольников DAC и KOD и равенству OD и OL , будет DC: DA = OK: OL, следовательно, когда веса А и P обратно пропорциональны плечам OK и OL , составляющим продолжения одно другого, то их действия равносильны, и они будут находиться в равновесии; это и есть известное свойство весов, рычага и ворота. Когда который-нибудь из двух грузов будет больше, нежели в этом отношении, то и усилие к вращению колеса будет соответственно больше.

Пусть груз р , коего вес равен весу груза Р , отчасти подвешен на нити Np , частью же поддерживается наклонною плоскостью G .

Если провести прямые рН и NH соответственно перпендикулярно горизонтальной плоскости и плоскости G , то представив через рН направленную вниз силу, равную весу груза p , можно ее разложить на силы pN и HN .

Если плоскость Q , пересекающая данную плоскость G по горизонтальной прямой, будет взята перпендикулярно направлению нити pN и груз p поддерживался бы лишь этими двумя плоскостями, то он давил бы на эти плоскости с силами pN и HN , соответственно перпендикулярными этим плоскостям, т. е. на плоскость Q силою pN и на плоскость G силою HN . Поэтому, если убрать плоскость Q , чтобы груз натягивал нить, то так как нить, поддерживая груз, теперь заменяет убранную прочь плоскость Q , то она будет натянута с тою самою силою pN , которая раньше давила на плоскость. Следовательно, натяжение этой наклонной нити будет так относиться к натяжению отвесной нити NP , как длина pN к рН . Поэтому, если отношение веса груза p к весу груза А будет равно отношению, составленному из отношения длин рН к pN и обратного отношения кратчайших расстояний от центра колеса до нитей подвеса pN и AM этих грузов, то их действия на колесо будут одинаковы, и они будут взаимно уравновешиваться, что всякий может испытать.

Груз р , надавливающий на вышеуказанные две наклонные плоскости, находится в условиях, подобных тем, как клин, коего грани и были бы эти плоскости; следовательно, можно определить соотношение между силами клина и молота, а именно, давление на грань Q так относится к силе, действующей на клин по направлению прямой рН от веса ли его или от удара молота, как pN относится к рН , к давлению же на вторую грань G – как pN к NН .

Наконец, и сила винта найдется подобным же разложением, ибо он не что иное, как клин, вгоняемый рычагом.

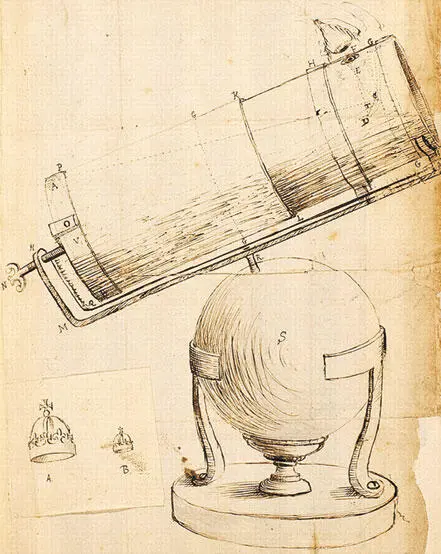
Рисунок Ньютона, изображающий схему первого отражающего телескопа, который он создал в 1668 году.

Применение этого следствия весьма широкое, и благодаря этому широкому применению постоянно обнаруживается справедливость его, ибо от вышесказанного зависит все учение о машинах, разными авторами излагаемое различным образом. Пользуясь этим же следствием, легко выводятся соотношения между усилиями в машинах, составленных из колес, барабанов, воротов, рычагов, блоков, натянутых канатов и других механизмов, и весами грузов, поднимаемых или прямо, или наклонно, а также силы связок, приводящих в движение кости животных.

Количество движения, получаемое из суммы количеств движения, когда они совершаются в одну сторону, и разность, когда они совершаются в стороны противоположные, не изменяется от взаимодействия тел между собою.

Так как по закону III действие и противодействие между собою равны и противоположны, то по закону II они производят равные изменения количеств движения, направленные в противоположные стороны. Таким образом, если движения двух тел направлены в одну сторону, то что приложится к количеству движения тела, идущего впереди, то вычтется из количества движения тела, за ним следующего, и сумма количеств движения обоих тел останется прежняя. Если же тела движутся в противоположные стороны, то вычтется поровну из количеств движения каждого из них, и следовательно, разность количеств движения, направленных в обратные стороны, останется без перемены.

Пусть масса шара А втрое больше массы шара В и скорость его заключает две части таких, коих скорость последующего за ним шара В заключает десять, и движение шаров происходит по той же самой прямой. Количества движения А и В будут относиться, как 6 к 10; положим, что эти количества соответственно равны 6 и 10 частям, так что сумма их равна 16. При встрече тел, если тело А приобретет количество движения, равное 3, 4 или 5 частям, то тело В утратит столько же частей, и следовательно, после отражения тело А пойдет, имея количество движения, равное 9, 10 или 11 частям, тело же В будет иметь или 7, или 6, или 5 частей, так что сумма все время остается равной 16, как и раньше. Если бы тело А приобрело 9, 10, 11 или 12 частей и, следовательно, после встречи шло бы, имея количество движения, равное 15, 16, 17 или 18, то тело В , потеряв столько же, сколько приобретено телом А , или идет вперед с 1 частью после потери 9, или находится в покое при потере 10 частей, или же идет назад, потеряв не только все свое количество движения, но еще (как сказано выше) и одну часть вдобавок, или же при потере 12 частей идет назад с количеством движения, равным 2. Таким образом суммы количеств движения, направленных в ту же сторону, как (15 +1) или (16 + + 0), и разности направленных в противоположные, как (17 – 1) или (18 – 2), составляют постоянно 16, как то было до встречи и отражения. Найдя количества движения, которыми обладают тела после отражения, определим и скорости каждого из них, ибо каждая из этих скоростей так относится к скорости, бывшей до удара, как количества движения соответствующего тела после и до удара. Так, например, для последнего случая тела А , коего количество движения до удара было равно 6 и скорость 2, после же отражения количество движения стало 18, скорость будет 6, как это следует из пропорции 18:6 = 6:2.

Когда тела не сферические или же, двигаясь по разным прямым, соударяются косвенно и требуется найти количества движения их после отражения, то необходимо сперва найти положение плоскости, касающейся обоих тел в точке их встречи, затем количество движения каждого тела разложить на два (по след. II), одно перпендикулярно сказанной плоскости, другое ей параллельно. Количества движения, параллельные плоскости, сохранятся без изменения, ибо взаимодействие тел происходит по прямой, перпендикулярной этой плоскости. Количества же движения перпендикулярные получают равные и противоположные изменения, так что сумма этих количеств движения, когда они направлены в одну сторону, и разность, когда они направлены в стороны обратные, остается тою же самою, какая была до удара. От отражений подобного рода могут происходить и вращательные движения тел около их собственных центров, но таких случаев я в дальнейшем не рассматриваю, и было бы весьма долго излагать все сюда относящееся.