Коллектив авторов - На плечах гигантов

Наиболее важное из того, что нам дает опыт о распределении материи, заключается в том, что относительные скорости звезд очень малы по сравнению со скоростью света. На этом основании я полагаю, что на начальном этапе в основу наших рассуждений можно положить приближенное допущение: пусть существует координатная система, относительно которой материю можно рассматривать находящейся в течение продолжительного времени в покое. По отношению к этой координатной системе контравариантный тензор материи T μν , в силу (5), имеет следующий простой вид:

(6)

Скаляр ρ (средней) плотности распределения изначально может быть зависимым от пространственных координат, но, предположив, что мир пространственно замкнут, мы можем сформулировать гипотезу о том, что ρ не зависит от места. Эту гипотезу мы положим в основу дальнейших рассуждений.

Что касается гравитационного поля, то из уравнения движения материальной точки

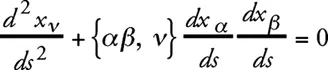
следует, что материальная точка в статическом гравитационном поле может находиться в покое только тогда, когда g 44не зависит от места. Так как, кроме того, мы для всех величин предполагаем независимость от временной координаты х 4, то для искомого решения можем потребовать, чтобы для всех x ν

Далее, как это обычно делается в статических задачах, примем, что

Остается определить те компоненты потенциала гравитационного поля, которые характеризуют чисто пространственно-геометрические свойства нашего континуума ( g 11, g 12, …, g 33). Из введенного допущения о равномерности распределения масс, создающих поле, следует, что и кривизна искомого метрического пространства должна быть постоянной. Таким образом, при заданном распределении масс искомый замкнутый континуум ( х 1, х 2, х 3при постоянном х 4) должен быть сферическим пространством.

Такое пространство можно получить, например, если исходить из евклидова пространства (ξ 1, ξ 2, ξ 3, ξ 4) четырех измерений с линейным элементом dσ . В этом случае

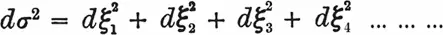
(9)

Рассмотрим в этом пространстве гиперповерхность

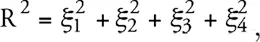
(10)

где R – постоянная. Точки этой гиперповерхности образуют трехмерный континуум – сферический объем с радиусом кривизны R .

Четырехмерное евклидово пространство, из которого мы исходили, служит только для удобного определения нашей гиперповерхности. Нас интересуют только точки этой поверхности, метрические свойства которой должны совпадать со свойствами физического пространства с равномерным распределением материи. Для описания этого трехмерного континуума воспользуемся координатами ξ 1, ξ 2, ξ 3(проекции на гиперплоскость ξ 4= 0), так как, в силу (10), можно ξ 4выразить через ξ 1, ξ 2, ξ 3. Исключая ξ 4из (9), получаем следующее выражение для линейного элемента сферического пространства:

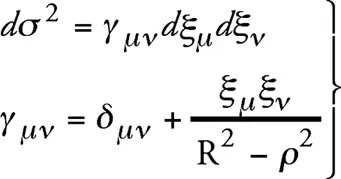
где δ μν = 1, если μ = ν , и δ μν = 0, если μ =/ ν,

.

Выбранные координаты удобны, когда речь идет об исследовании окрестности точки ξ 1= ξ 2= ξ 3= 0.

Итак, теперь у нас есть также и линейный элемент искомого четырехмерного пространственно-временного мира. Очевидно, для потенциалов g μν , у которых оба индекса отличаются от 4, мы должны написать

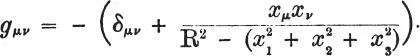
(12)

Полученное равенство вместе с соотношениями (7) и (8) вполне определяет свойства масштабов, часов и лучей света в рассматриваемом четырехмерном мире.

Приведенные выше рассуждения показывают, что теоретически можно построить материю только из гравитационного и электромагнитного полей, не вводя никаких гипотетических дополнительных членов в духе теории Ми. Эта возможность представляется особенно содержательной потому, что она освобождает нас от необходимости введения особой постоянной α для решения космологической проблемы. С другой стороны, присутствует и своеобразная трудность. Так, если применить уравнение (1) к случаю статического сферически симметричного поля, то мы получаем на одно уравнение меньше, чем нужно для определения g μν и Φ μ ν . Таким образом оказывается, что всякое распределение электричества, совместимое со сферической симметрией , может оставаться в равновесии. В настоящий момент проблему построения теории элементарных частиц нельзя решить на основе указанных уравнений поля.

Стивена Хокинга считают вторым по гениальности физиком-теоретиком после Эйнштейна. Он много сделал для популяризации науки: его книга «Краткая история времени» переведена на 40 языков и разошлась общим тиражом в 10 миллионов экземпляров. Читатели хорошо приняли и другие книги, в том числе написанные в соавторстве с другими учеными.

Хокинг родился в Оксфорде 8 января 1942 года (спустя ровно 300 лет после смерти Галилея). Он изучал физику в Университетском колледже, получил докторскую степень по космологии в Кембридже и с 1979 года занимал пост лукасовского профессора математики. Эту должность создали в 1663 году на средства преподобного Лукаса Генри, члена парламента от Кембриджского университета. Первым лукасовским профессором был Исаак Барроу, а затем, в 1669 году, кафедру занял Исаак Ньютон. Эту должность присуждают тем, кого считают самым выдающимся мыслителем своего времени.

Профессор Хокинг изучал фундаментальные законы, управляющие Вселенной. Совместно с Роджером Пенроузом он показал, что из эйнштейновской общей теории относительности следует, что у времени и пространства было начало – Большой взрыв – и бывает конец – черная дыра. Рассчеты показали, что необходимо объединить ОТО и квантовую механику – еще одно великое научное достижение первой половины ХХ века. В числе следствий подобного объединения было открытие Хокинга: черные дыры не могут быть абсолютно черными, они излучают и впоследствии испаряются. Кроме того, Хокинг сделал вывод, что у Вселенной нет ни края, ни границы в мнимом времени.