РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Название:Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров
- Автор:
- Жанр:
- Издательство:Альпина Паблишер
- Год:2007
- ISBN:ISBN 978-5-9614-0610-8
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
РАЛЬФ РАЛЬФ ВИНС - Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров краткое содержание
Математика управления капиталом. Методы анализа риска для трейдеров и портфельных менеджеров - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Отметьте, что мы используем модель ценообразования фондовых опционов. Для волатильности будем использовать значение OV. Если безрисковая ставка R = 6% и доля года, оставшаяся до истечения срока, Т = 0,25, то из (5.03) получим:

Полученное значение подставим в уравнение (5.05). Теперь для расчета дельты колл-опциона решим уравнение (3.21):


Подставим значения Y и N'(1,967087528) в уравнение (3.21) для получения дельты колл-опциона, в соответствии с уравнением (5.05):


Таким образом, когда цена портфеля равна 100, цена исполнения 100, доля года, оставшаяся до истечения срока исполнения, составляет 0,25, безрисковая ставка равна 6%, а волатильность портфеля 785,3069464%, дельта нашего гипотетического колл-опциона равна 0,9754135259. Сумма весов геометрического оптимального портфеля, состоящего из Toxico, Incubeast и LA Garb, найденная из уравнения (8.05), составляет 1,9185357. Таким образом, принимая во внимание уравнение (8.06), при страховании портфеля мы можем переразмещать до 50,84156244% (0,9754135359/ /1,9185357). Во сколько обходится страхование? Все зависит от волатильности в течение срока действия смоделированного опциона. Например, если за время действия смоделированного опциона баланс на счете не колеблется (волатильность равна 0), цена смоделированного опциона, т.е. стоимость страхования, равна нулю. В этом заключается большое преимущество страхования портфеля по сравнению с реальной покупкой пут-опциона (если этот пут-опцион по портфелю существует). Мы платим теоретическую цену опциона, исходя из той волатильности, которой реально подвержен портфель, а не той, которая существовала на рынке до открытия позиции, как бывает при покупке пут-опциона. Кроме того, реальная покупка пут-опциона (опять же, если пут-опцион по нашему портфелю существует) влечет за собой расходы, связанные со спредом покупки/продажи. При моделировании опциона таких расходов не возникает.
Необходимые залоговые средства
Мы видели, что при добавлении рыночной системы портфель улучшается, если коэффициент линейной корреляции изменений дневного баланса между этой рыночной системой и другой рыночной системой в портфеле меньше +1, поскольку в этом случае повышается среднее геометрическое дневных HPR. Таким образом, логично использовать как можно больше рыночных систем. Естественно, на каком-то этапе может возникнуть проблема с залоговыми средствами. Проблема, связанная с нехваткой залоговых средств, может возникнуть даже в том случае, если вы используете только одну рыночную систему. Как правило, оптимальное долларовое f меньше первоначальных залоговых требований для данного рынка. Если же доля f очень высока (неважно, используете вы стратегию статического или динамического дробного f), вы можете столкнуться с требованием довнесения залога (margin call), в противном случае позиция будет принудительно закрыта. Если вы используете портфель рыночных систем, требование дополнительного внесения залога становится еще более вероятным. В неограниченном портфеле сумма весов часто значительно больше 1. Когда вы используете только одну рыночную систему, вес де-факто равен единице. Если сумма весов рыночных систем равна, например, трем, тогда вероятность требования внесения залога в три раза выше, чем в случае торговли только на одном рынке. Оптимальный портфель следует создавать с учетом минимально необходимых залоговых средств для компонентов портфеля. Это достаточно легко сделать: надо определить, какую долю f вы можете использовать в качестве верхней границы U; ее можно найти с помощью уравнения (8.08):
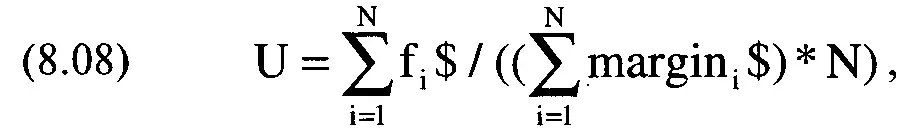
где U = верхняя граница дробного f, при которой можно торговать оптимальным портфелем без риска получения требования довнесения залога;
f$= оптимальное долларовое f для рыночной системы i;
margin $ = первоначальный залог для рыночной системы i;
N = общее число рыночных систем в портфеле.
Если U больше единицы, то приравняйте U к единице. Например, у нас есть портфель из трех рыночных систем со следующими оптимальными долларовыми f и первоначальными минимальными залоговыми требованиями (примечание: f$ являются оптимальными долларовыми f для каждой рыночной системы портфеля, они представляют собой оптимальные f рыночных систем, деленные на соответствующие веса в портфеле):
| Рыночная система | f$ | Первоначальный залог |
| А | $2500 | $2000 |
| В | $2000 | $2000 |
| С | $3000 | $2000 |
| Суммы | $7500 | $6000 |
В соответствии с уравнением (8.08) мы возьмем сумму всех f$ (7500 долларов) и разделим ее на сумму первоначальных залоговых требований (6000 долларов), умноженную на число рынков N:
U = $7500 / ($6000 * 3) =7500/18000 =0,4167
Таким образом, доля f не должна превышать 41,67% (если мы применяем стратегию динамического дробного f), т. е. следует производить переразмещение, когда отношение активного баланса к общему балансу больше или равно 0,4167.
Если вы все-таки применяете стратегию статического дробного f (несмотря на все ее недостатки), тогда максимальное значение используемой доли должно быть равно 0,4167. Такой подход сместит вас по геометрической эффективной границе портфелей с неограниченной суммой весов влево от оптимального портфеля, но вы будете настолько близко к нему, насколько только возможно, чтобы не столкнуться при этом с требованием довнесения залога. Для примера рассмотрим счет в 100 000 долларов. Если доля f равна 0,4167, то для каждой рыночной системы получим:
| Рыночная система | f$ | /0,4167= | Новое И |
| А | $2500 | $6000 | |
| В | $2000 | $4800 | |
| С | $3000 | $7200 | |
При счете в 100 000 долларов мы будем торговать 16 контрактами рыночной системы А (100 000/6000), 20 контрактами рыночной системы В (100 000/4800) и 13 контрактами рыночной системы С (100 000/7200). Итоговое требование к залогу для такого портфеля равно:
16 * $2000 = $32 000 20 * 2000 = 40 000 13 * 2000 = 26 000
Первоначальное требование залога $98 000
Читать дальшеИнтервал:
Закладка:










