Игорь Брыгов - Шахматы. Первое приближение

В средней школе изучается так называемая евклидовая геометрия. Одна из основных аксиом (утверждений, не подлежащих ревизии, пересмотру) которой, следующая: кратчайшим расстоянием между двумя точками – является одна прямая линия. На шахматной доске таких прямых может быть несколько (от одной до 357 – движение от поля е1до поля е8). Движение фигур может и осуществляется как по традиционным прямым, так и по ломаным линиям. Общее расстояние при этом не меняется.

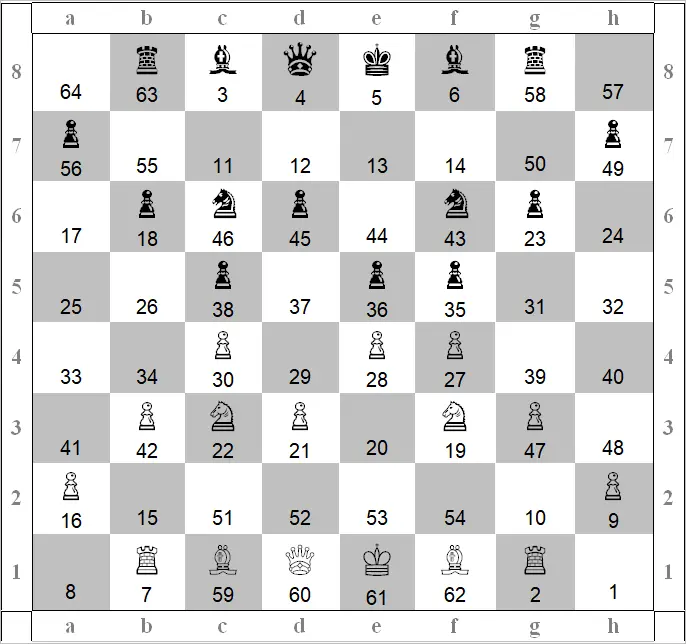
Диаграмма 2

Эта позиция на доске возникла на доске после ходов:

1) d3– d6; 2) e3– e6; 3) b3– b6; 4) g3– g6; 5) c3– c6; 4) f3– f6; 5) c4– c5; 6) f4– f5; 7) Kc3– Kc6; 8) Kf3– Kf6; 9); Лb1– Лb8; 10) Лg1– Лg8.

Она носит название «табия “Альмуджаннах”». Мы видим магический квадрат, где сумма чисел каждой строки каждого столбца, а также двух главных диагоналей равна 260. Этот же рисунок, только без фигур, будет предметом дальнейшей работы. Итак.

Что видимо – принцип построения квадрата есть, и его построение таково: в углах доски правый нижний и левый верхний – соответственно, начало и конец нумерации полей цифры 1 и 64 = 65, левый нижний и правый верхний 8 и 57 = 65. Записывая углы, соседние цифры записываем по ходу ряда, соответственно, 63, 58, 2, 7. Верхний ряд – промежуток между углами 3, 4, 5, 6. Нижний ряд – промежуток между углами 59, 60, 61, 62. Второй нижний ряд – к первому ряду прибавляем или отнимаем 8 (только без отрицательных значений и суммы цифр больше 65). Седьмой ряд – отнимаем или прибавляем цифру 8 (только без отрицательных значений и сумму цифр больше 65). Внутренние четыре ряда заполняем, отталкиваясь от поля h7–49, h3–48, g3–47, a3–41, b3–42, и поднимаясь выше – (минус) 8. Внутренний квадрат 4 на 4 с поля f3–19 по строчке 20, 21, 22 и +(плюс) 8 на каждое поле вверх. Вывод: поля равнозначные следующие (по парам):

h1 – a8, g1 – b8, a1 – h8, b1 – g8, c8 – f1, d8 – e1, e8 – d1, f8 – c1, h2 – a7, g2 – b7, f2 – c7, e2 – d7, d2 – e7, c2 – f7, b2 – g7, a2 – h7, h3 – a6, b6 – g3, c6 – f3, c3 – f6, d3 – e6, e3 – d6, b3 – g6, a3 – h6, a4 – h5, b4 – g5, c4 – f5, d4 – e5, e4 – d5, f4 – c5, g4 – b5, h4 – a5.

Вывод: если фигура (пешка) находится на равнозначном поле, проиграть оппоненту она не должна.

1. Какому полю соответствует поле с4?

2. Какому полю соответствует поле f5?

3. Какому полю соответствует поле h6?

4. Какому полю соответствует поле е4?

5. На доске стоят две одинаковые фигуры. Белый король на поле g2и черный король на поле b7. Конгруэнтна ли (одинаково расположена) эта пара фигур? Найдите другое (симметричное поле) для черного короля.

6. Король белых стоит на поле e3. Где должен стоять король черных, чтобы не проиграть партию (сделать ничью)? Найдите еще один вариант решения шестого вопроса.

7. На доске находятся 6 пешек: белые – h2, g2, f2; черные – a7, b7, c7. Они никогда не встретятся и не пересекутся в качестве пешек. Первый ход одной из белых пешек. Как вы считаете, кто победит?

8. Расстояние от поля e1до поля e8–7 полей (8–1 =7). Придумайте ломаную линию, длина которой будет равна 7 полям, или несколько таких линий.

В первой главе мы познакомились с волшебным квадратом: пары соответствия полей мы должны выучить наизусть, они нам всегда пригодятся. Есть теории, что шахматы (точнее, доска, произошли от древнейших математических таблиц, связанных с вычислениями. Реальные свидетельства у нас имеются: шахматная доска или ее полный аналог (большее число полей) использовалась в древности в строительстве египетских пирамид, а южноамериканские пирамиды выглядят с космоса как точная калька шахматной доски. В другой ипостаси: военный симулякр (создание плана (-ов) реальных военных сражений) – это Индия. Игра (шахматы) – называлась чатуранга, в дословном переводе «сражение четырех родов войск» (пехота, конница, боевые слоны, осадные (боевые) башни). Учитывая реальную эффективность использования чатуранги как боевого тренажера, игра стала расти главным образом через персидские, позже арабские, завоевания. Самоназвание игра получила в Персии (версий несколько), в дословном переводе: король (шах) умер (мат), буква «ы» – русский довесок. Одному из царей игра так понравилась, что он решил наградить человека (версий рассказа несколько), который его с ней познакомил. Награду предложено было выбрать награждаемому. Тот скромно попросил засыпать доску пшеницей в размере 2 в 64-й степени (первый известный пример упоминания геометрической прогрессии). Почему скромно? Чтобы вырастить такое количество пшеницы, ее надо сажать, выращивать, собирать (и не съесть ни зернышка) на всей планете Земля в течение приблизительно 300 лет. С практической (человеческой) точки зрения – эту величину уже можно принимать за бесконечность, но как бы бесконечен ни был ареал обитания (шахматная доска), он только среда. Для кого? Очевиден ответ: в первую очередь, для подобия (копии) человека.

Составим список понятий.

Дефиниции (определения) будут следующие.

1. Игрок-бог (творец) сотворил. «И вышла на берег, перстами пылая – прекрасная Эа». Александр Сергеевич Пушкин.

2. Эа (Гея) – земля – шахматная доска. И создал Бог землю, и сказал: «Это хорошо». И создал Бог ночь и день (черное и белое).

3. Человек на земле – фигура, именуем его – Адам(доля шутки) – король.

4. Передвижение человека по имени ( Адам) Король по земле – один шаг – одно поле.

5. Куда передвигается? В каком направлении? В любом (горизонталь, вертикаль, горизонталь).

Удивительно, но, если посмотреть на все живое, за редким исключением, все виды живых организмов симметричны. Левая половинка = правая половинка. Нам присуще чувство прекрасного – которое оказывается при ближайшем рассмотрении очаровательной симметрией форм и звуков. Классическая музыка – подозрительно похожа на биологическое магнитное излучение здорового живого организма – ауры (в ритмическом волновом сравнении). Строение известного макрокосмоса – увеличенная копия микрокосмоса. И симметрия – всегда минимум пара. И, следуя законам симметрии, – королей всегда два.

Но вот незадача. И боги ошибаются. Короли получились разных знаков + (плюс) и – (минус).