Александр Полулях - Грохочение угля

Таблица 1.6

Уравнения гранулометрических характеристик крупности частиц

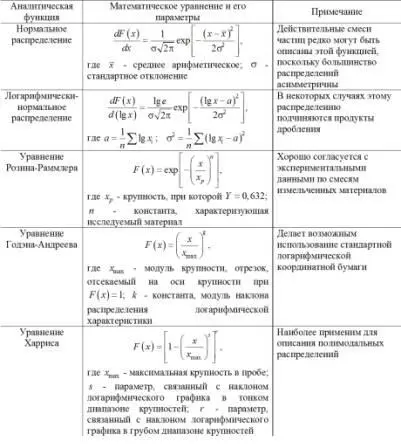
Уравнение Розина-Раммлера охватывает опытные точки в широком диапазоне крупностей, но оно не удовлетворяет одному конечному условию: нулевой выход классов достигается только при бесконечно большой крупности материала

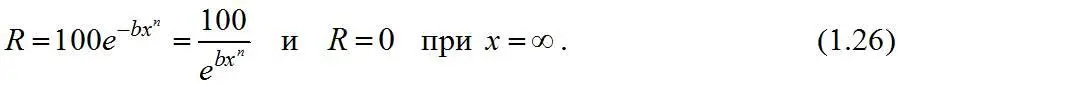
При использовании уравнения Розина-Раммлера приходится считаться с этим обстоятельством и принимать конечную крупность материала, соответствующую какому-то определенному значению выхода класса.

В табл. 1.6 приведены наиболее известные уравнения гранулометрических характеристик частиц.

Кривые распределения показывают, число частиц или весовые выхода каждого класса крупности в данном материале. Материал, состоящий из смеси частиц разных размеров, разделенный на классы по крупности, можно рассматривать как статический коллектив. Размер частиц будет аргументом коллектива, а общее число частиц в пробе материала или ее общий вес составят числовой или весовой объем статического коллектива. Число частиц в каждом классе или их вес называют численностью класса, частотой или абсолютной частностью, а частоты классов, отнесенные к объему коллектива, – относительными частностями классов.

Если в прямоугольных координатах по оси абсцисс откладывать крупность классов и на соответствующих интервалах крупности построить прямоугольники, площади которых будут пропорциональны частоте класса, то получим гистограмму распределения зерен материала.

Это равнозначно построению прямоугольников высотой, равной частности на единицу длины интервала, на интервале, как основании прямоугольника. При уменьшающемся интервале ступенчатая линия, сверху ограничивающая прямоугольники, приближается к плавной кривой и в пределе дает кривую распределения (рис. 1.14). Ординаты кривой распределения выражают частность на единицу длины бесконечно узкого интервала по оси абсцисс, а площадь под кривой определяет число объектов (число частиц, весовой выход их) в соответствующих промежутках.

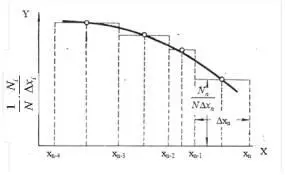
Рис. 1.14. Кривая распределения по числу частиц

Таким образом, для построения кривой распределения по числу частиц следует по оси абсцисс на интервале x n - x n -1 построить прямоугольник высотой

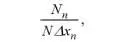
Затем построить прямоугольники для всех других классов и соединить кривой точки на серединах верхних сторон прямоугольников. Относительное число частиц в бесконечно малом интервале dx будет

и в классе x n - x n -1

Аналогично строится кривая распределения частностей весовых выходов. Кривые распределения дают более наглядное представление о гранулометрическом составе сыпучих материалов в сравнении с суммарными характеристиками крупности. В классах с наибольшим выходом кривая показывает максимум, а при отсутствии в материале частиц какого-либо размера – падает до нуля. Выхода класса на кривой распределения пропорциональны площадям, ограниченным кривой и двумя ординатами, проведенными на диаметрах, ограничивающих данный класс.

Кривые распределения и суммарной характеристики крупности полностью характеризуют гранулометрический состав материала с точки зрения математической статистики. Возможен аналитический переход от одной кривой к другой, если известно уравнение какой-либо из них.

Если известно уравнение суммарной характеристики крупности, то общий ход вычисления поверхности и числа частиц может быть принят следующий.

Пусть уравнение характеристики «по минусу» будет

где y – выход частиц меньше диаметра x , см.

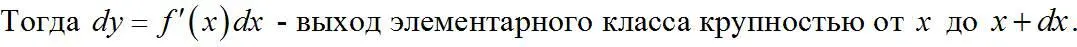
В 1 г материала с плотностью δ г/см 3объем элементарного класса составит

Для одной частицы кубической формы объем равен x 3 , а поверхность 6 x 2 .

Число частиц в элементарном классе

а поверхность частиц

Число частиц и их поверхность в классе мельче x 2 и крупнее x 1 находятся интегрированием этих выражений в пределах от x 1 до x 2

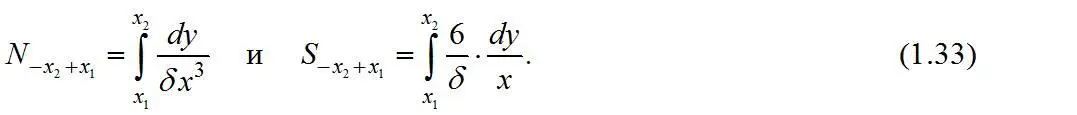
При вычислении поверхности безразлично, будет ли принята форма частиц за куб или за шар. В самом деле, если принять все частицы шарообразной формы, то получим

Уравнение Розина-Раммлера для суммарной характеристики крупности «по минусу»

где y – суммарный выход класса минус x мк в долях единицы, остальные обозначения см. формулу (1.20).

Уравнение кривой распределения

Число частиц в бесконечно узком классе, содержащемся в 1 г материала,

Поверхность частиц бесконечно узкого класса, содержащегося в 1 г материала,