Александр Полулях - Грохочение угля

Если набор сит, применяемых для ситового анализа, имеет постоянный модуль, то построение полулогарифмической характеристики значительно упрощается, так как отрезки на оси абсцисс будут одинаковой величины. Например, для ряда сит с постоянным модулем М разница между логарифмами размеров смежных сит составит:

Каждый отрезок на оси абсцисс между соседними ситами равен lgM . При построении характеристики за lgM можно принять произвольный отрезок.

Полулогарифмические суммарные характеристики крупности (по данным табл. 1.3) показаны на рис. 1.11. В отличие от обыкновенных кривых суммарной характеристики, левая ветвь полулогарифмических кривых не доходит до ординаты, соответствующей выходу 100 %, так как этому выходу по оси абсцисс соответствует lg0=- ∞.

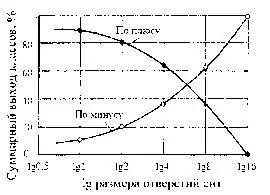
Рис. 1.11. Полулогарифмические суммарные характеристики крупности

Логарифмическая суммарная характеристика крупности строится в системе координат (lgx; lgy) , где x=l – размер отверстий сита, y – суммарный выход классов.

Логарифмическая характеристика позволяет, в некоторых случаях, установить наличие закономерности распределения в материале зерен по крупности.

Для дробленных и измельченных мономинеральных пород логарифмическая характеристика, построенная «по минус l », большей частью получается прямолинейной. Пример построения логарифмической суммарной характеристики крупности (по данным табл. 1.3) показан на рис. 1.12.

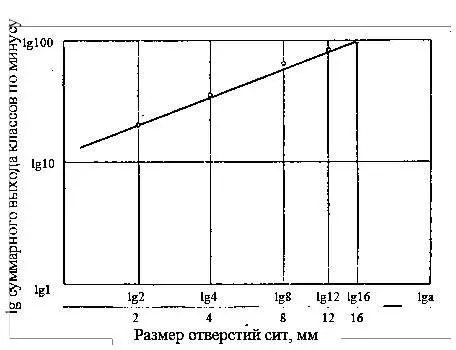
Рис. 1.12. Логарифмическая суммарная характеристика крупности

Если логарифмическая суммарная характеристика по минусу прямолинейная, то для такого материала гранулометрический состав можно представить уравнением.

Уравнение прямой линии в логарифмических координатах

Переходя к антилогарифмам, получим

Это уравнение суммарной характеристики, построенной «по минус х », известно под названием уравнения Годэна-Андреева [3].

Величина показателя k определяет направление и степень изгиба кривой характеристики. Если характеристику построить «по плюс x », то она будет: при k>1 – выпуклой, при k=1 – прямой, при k<1 – вогнутой. Следовательно, по величине показателя k можно судить о преобладании в материале крупных или мелких зерен.

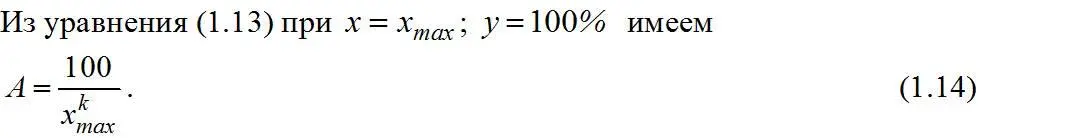
Величина параметра А , при данном показателе k , зависит от величины x max (диаметра максимального зерна материала).

Уравнение характеристики позволяет решать ряд задач, например: определять число зерен в любом классе, поверхность зерен, удельную поверхность и т. п.

Параметры уравнения находятся следующим образом. На логарифмической характеристике выбираются две точки, соответствующие двум наиболее удаленным диаметрам, и определяется показатель k как тангенс угла наклона прямой

Параметр А находится подставкой значения k в уравнение (1.12) для одной из точек.

Если диаметр зерен брать по отношению к диаметру максимального куска в материале, то уравнение Годэна-Андреева преобразуется в «приведенное» уравнение с одним постоянным параметром

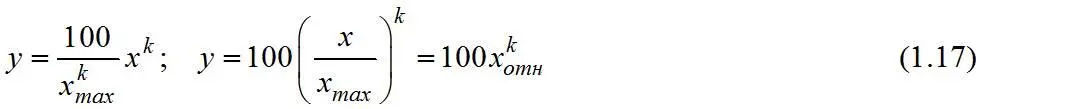
или, если y выражено в долях единицы, то

Показатель k находят описанным выше вычислением или, если принять за исходные для расчета x 2и x 1=1/2x 2, то

Обработка большого количества гранулометрических анализов продуктов дробления и измельчения показала, что во многих случаях лучшее соответствие опытным данным, по сравнению с уравнением Годэна-Андреева, дает уравнение, предложенное Розиным и Раммлером [3]

где R – суммарный выход класса крупнее х (по плюсу), %; x – размер отверстий сита; b и n – параметры, зависящие от свойств материала и размерности величины х .

Соответствие опытных данных уравнению (1.20) можно проверить графическим путем нанесения опытных точек на функциональную координатную систему. При двойном последовательном логарифмировании уравнения (1.20) последнее приобретает вид

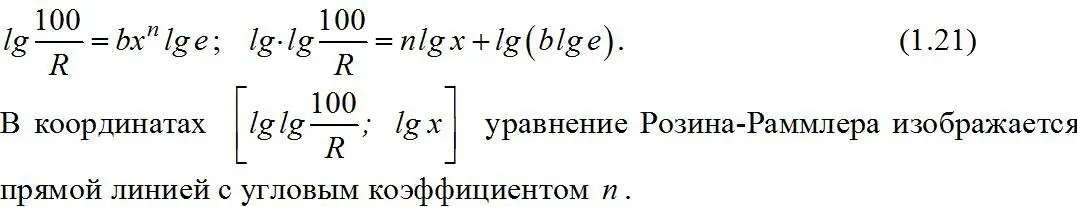
Пример построения такого графика (по данным табл. 1.5) показан на рис. 1.13.

Таблица 1.5

Гранулометрический состав исследуемого материала

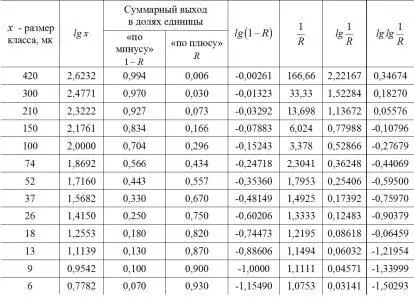
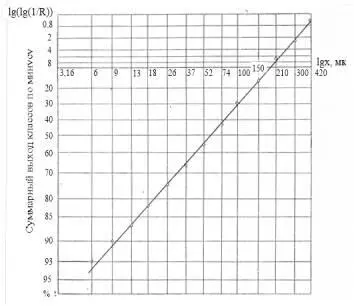
Рис. 1.13. Характеристика крупности по Розину и Раммлеру

На осях против соответствующих логарифмических величин написаны значения выходов классов и диаметров зерен материала.

Параметры уравнения (1.20) b и n находят по двум известным точкам, решая систему уравнений:

При совместном решении получим

что, впрочем, можно написать и сразу по графику рис. 1.13. Зная n , определяем b :

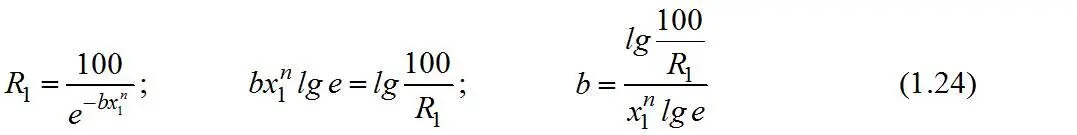
Для примера по данным табл. 1.5 составлено следующее уравнение характеристики крупности материала: